| Issue |
Manufacturing Rev.
Volume 4, 2017
|
|
|---|---|---|
| Article Number | 6 | |
| Number of page(s) | 9 | |
| DOI | https://doi.org/10.1051/mfreview/2017005 | |
| Published online | 23 May 2017 | |
Research Article
Microstructure-sensitive flow stress modeling for force prediction in laser assisted milling of Inconel 718
1
Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA
30332, USA
2
Metal Industries Research and Development Centre (MIRDC), Kaohsiung
811, Taiwan
* e-mail: steven.liang@me.gatech.edu
Received:
23
March
2017
Accepted:
21
April
2017
Inconel 718 is a typical hard-to-machine material that requires thermally enhanced machining technology such as laser-assisted milling. Based upon finite element analysis, this study simulates the forces in the laser-assisted milling process of Inconel 718 considering the effects of grain growth due to γ' and γ" phases. The γ" phase is unstable and becomes the δ phase, which is likely to precipitate at a temperature over 750 °C. The temperature around the center of spot in the experiments is 850 °C, so the phase transformation and grain growth happen throughout the milling process. In the analysis, this study includes the microstructure evolution while accounting for the effects of dynamic recrystallization and grain growth through the Avrami model. The grain growth reduces the yield stress and flow stress, which improves the machinability. In finite element analysis (FEA), several boundary conditions of temperature varying with time are defined to simulate the movement of laser spot, and the constitutive model is described by Johnson-Cook equation. In experiments, this study collects three sets of cutting forces and finds that the predicted values are in close agreements with measurements especially in feed direction, in which the smallest error is around 5%. In another three simulations, this study also examines the effect of laser preheating on the cutting forces by comparison with a traditional milling process without laser assist. When the laser is off, the forces increase in all cases, which prove the softening effect of laser-assisted milling. In addition, when the axial depth of milling increases, the laser has a more significant influence, especially in axial direction, in which the force with laser is more than 18% smaller than the one without laser. Overall, this study validates the influence of laser-assisted milling on Inconel 718 by predicting the cutting forces in FEA.
Key words: Inconel 718 / Laser-assisted milling / FEA / Recrystallization
© Z. Pan et al., Published by EDP Sciences, 2017
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Inconel 718 is a nickel-based super alloy with high hardness of HRC 30–40 and high melting temperature about 1300 °C. Because of these properties, Inconel 718 is a typical hard-to-machine material. Machining this material in a conventional way normally results in extreme high cutting forces [1, 2]. To reduce the forces as well as tool wear, researchers have introduced several thermally enhanced machining technologies such as laser-assisted milling. The intense beam produced by laser increases the temperature in the region in front of cutting tool and therefore drops the flow stress and strain-hardening rate, leading to lower cutting forces [3, 4]. Shi et al. [5] evaluated the machinability of Inconel 718 after laser-assisted machining and concluded that cutting forces decreased by 18% in their experiments. In addition to direct experiment measurements, finite element analysis (FEA) is another popular method for examining the material properties and cutting parameters during laser-assisted milling. Nyon et al. [6] used ANSYS to simulate the laser-cutting process on Inconel 718. They modeled the Gaussian-distributed heat flux when laser-beam heating the workpiece, but they neglected microstructure evolution. Wasle et al. [7] used DEFORM to simulate the microstructure development during hot forming processes. They applied Avrami-type equations to predict dynamic and metadynamic recrystallized fractions. Our study is similar to their work, but it focuses on laser-assisted milling and force prediction. Rahim et al. [8] used ANSYS Parametric Design Language to predict the laser beam-to-cutting tool distance and temperature distribution. Most of their conclusions pertained to the movement between the laser beam and the workpiece, but they only qualitatively analyzed the resultant material properties and cutting parameters such as surface roughness and the undeformed chip thickness. In addition, they made no comments on cutting forces. Using the commercial software ABAQUS, Balbaa and Nasr [9] predicted cutting forces in both conventional and laser-assisted machining and compared their simulation results to those of Shi et al. [5]. Nevertheless, their study was limited to 2D orthogonal cutting, and this study expands the simulation to 3D.
Microstructure evolution, which occurs in both the chip and the machined surface of Inconel 718, includes grain size changes, textures changes, and grain misorientations [10]. Among these factors, grain growth and phase transformation, which have been studied for a long time, are important in the study of microstructure evolution. The grain growth of nickel-based super alloys such as Inconel 718 is mainly due to γ' and γ" phases. The γ" phase is unstable and becomes the δ phase, which precipitates at a temperature of over 750 °C [11]. The main phase transformation occurs during the dynamic recrystallization (DRX) process. Using DEFORM, Reshetov et al. [12] simulated the hot extrusion operation of ATI 718Plus® alloy, a nickel-based super alloy, and they used embedded grain growth and recrystallization models to show microstructure evolution. Similarly, this study uses the models of grain growth and DRX embedded into DEFORM. Section two introduces the Avrami recrystallization model [13, 14], which describes grain growth and DRX, and Section three introduces the single-beam coaxial laser-assisted milling spindle for experiment validation. Section four validates the model by presenting the simulation and experiment results and compares simulated cutting forces with laser preheating to those without laser preheating. Laser preheating temperature differentiates the non-laser assisted milling (non-LAM) and LAM. And the grain growth and microstructure evolution are included in both cases. The novelty of this work is the comparison between non-LAM and LAM when the grain growth and microstructure evolution are considered.
2. Mechanically and thermally induced recrystallization model
Unlike previous studies, this study examines the evolution of a microstructure evolution in the context of grain growth attributed to phase transformation. Many researchers have studied microstructure evolution in several machining processes. Pan et al. [14] simulated the microstructure evolution during hot forging. They predicted the recrystallized grain size and compared the simulations to measurements. Pan et al. [15] investigated the grain size effect in the machining process of titanium alloys. Loyda et al. [16] evaluated the average grain size and recrystallization during the rotary forging process. The average grain size changing with time at different temperature was plotted. The distribution of average grain size after the process was studied. Both forging and laser-assisted milling have high temperature around 1000 °C and large plastic deformation, so similar microstructure evolution process is studied in this work.
During the milling process, the thermal and mechanical energies transfer to the stored energy in a dislocation substructure that provides the driving forces for grain growth or recrystallization. The nucleation and subsequent grain growth reduce the energy, when the grain boundary area is smaller. The γ' (Ni3Al) and γ" (Ni3Nb) phases contribute to the hardening of Inconel 718. At a temperature of over 750 °C, the metastable γ" phase transfers to stable δ (Ni3Nb) phase that controls the grain size during laser-assisted milling. The microstructure evolution is classified as recrystallization and grain growth, and the recrystallization is treated as dynamic recrystallization (DRX), static recrystallization (SRX), and metadynamic recrystallization (MDRX). During the deformation, when the temperature reaches the phase transformation temperature and the effective plastic strain is larger than the threshold value, the DRX occurs. If DRX starts with nucleation but is unable to complete during the deformation, the recrystallization finishes after deformation and it is called MDRX. When the recrystallization occurs after deformation since the effective plastic strain is always smaller than the threshold value, the SRX happens without nucleation. The transformation follows a characteristic s-shaped profile where the rates are low at two ends but rapid in the middle.
Because DRX is main microstructure evolution process, this study involves DRX and grain growth in simulation. The Avrami equation describes the kinetics of crystallization at constant temperature, and this study uses the embedded Avrami recrystallization model to predict grain growth and DRX. To apply this model, this study assumes the random distribution of nucleation and grain growth. Predicted average grain size d is a function of the dynamically recrystallized average grain size and the recrystallized volume fraction: (1)where d0 is the constant initial average grain size selected to be 10 μm, ddrex is the dynamically recrystallized average grain size calculated from the grain size model, and Xdrex is the recrystallized volume fraction from a kinetics calculation. Dynamically recrystallized average grain size ddrex is:
(1)where d0 is the constant initial average grain size selected to be 10 μm, ddrex is the dynamically recrystallized average grain size calculated from the grain size model, and Xdrex is the recrystallized volume fraction from a kinetics calculation. Dynamically recrystallized average grain size ddrex is: (2)where a8, h8, n8, m8, and c8 are the material constants listed in Table 1. In addition, R is the gas constant, Qact is the activation energy,
(2)where a8, h8, n8, m8, and c8 are the material constants listed in Table 1. In addition, R is the gas constant, Qact is the activation energy,  is the plastic strain,
is the plastic strain,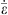 is the plastic strain rate, and T is the temperature. From the aspect of dynamic recrystallization kinetics, the recrystallized volume fraction is:
is the plastic strain rate, and T is the temperature. From the aspect of dynamic recrystallization kinetics, the recrystallized volume fraction is:![$$ {X}_{\mathrm{drex}}=1-\mathrm{exp}\left[-{\beta }_d{\left(\frac{\overline{\epsilon }-{a}_{10}{\epsilon }_p}{{\epsilon }_{0.5}}\right)}^{{K}_d}\right], $$](/articles/mfreview/full_html/2017/01/mfreview170004/mfreview170004-eq5.gif) (3)where βd, a10, and Kd are material constants. a10εp is the critical strain to start the recrystallization when the deformation across a nucleus. At this point, the growth of the first nuclei is under softening locally, but the other parts of the workpiece continue to harden. For this study, a10 is 0.8, so the critical strain is estimated as 0.8 of the peak strain. Peak strain εp is:
(3)where βd, a10, and Kd are material constants. a10εp is the critical strain to start the recrystallization when the deformation across a nucleus. At this point, the growth of the first nuclei is under softening locally, but the other parts of the workpiece continue to harden. For this study, a10 is 0.8, so the critical strain is estimated as 0.8 of the peak strain. Peak strain εp is: (4)where a1, h1, m1, and c1 are material constants. ε0.5 is the strain that yields Xdrex = 0.5,
(4)where a1, h1, m1, and c1 are material constants. ε0.5 is the strain that yields Xdrex = 0.5, (5)where a5, h5, n5, m5, and c5 are material constants. The grain growth model describes the grain size change without the influence of strain or strain rate,
(5)where a5, h5, n5, m5, and c5 are material constants. The grain growth model describes the grain size change without the influence of strain or strain rate,![$$ {d}_{{gg}}=[{d}_0^m+{a}_9{t}\enspace \mathrm{exp}(-{Q}_9/{RT}){]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$m$}\right.}, $$](/articles/mfreview/full_html/2017/01/mfreview170004/mfreview170004-eq8.gif) (6)where a9, m, and Q9 are material constants, t is time. Avrami model parameters are listed in Table 1. These parameters are obtained from both DEFORM default settings and Huang et al. [16], Reyes et al. [17], and Loyda et al. [18].
(6)where a9, m, and Q9 are material constants, t is time. Avrami model parameters are listed in Table 1. These parameters are obtained from both DEFORM default settings and Huang et al. [16], Reyes et al. [17], and Loyda et al. [18].
Inconel 718 material constants of the Avrami recrystallization model.
3. Simulation modeling and experimental validation
This study predicts the laser-assisted half-slot milling process, shown in Figure 1, using the commercial FEA software DEFORM v11.1 (Scientific Forming Technologies Corporation, Columbus, OH). This study validates the simulation results by conducting experiments on the single-beam coaxial laser-assisted milling spindle, illustrated in Figure 2. The spindle speed was 3000 rpm, the helix angle was 35°, and the tool diameter was 6 mm. To prove the availability, this study selects the feed rate and the axial depth of milling to be two variables for comparison, shown in Table 2, and simulates three extra milling processes without laser preheating, which shows improvement in the machinability of Inconel 718. Therefore, it presents six simulations and three experiments. The mechanical and thermal properties of Inconel 718 are listed in Table 3 [19].
 |
Figure 1. Schematic diagram of half-slot milling, the cross indicates the instantaneous center location of a laser with a radius of 0.7 mm. |
 |
Figure 2. Experimental setup of the single beam coaxial laser-assisted milling spindle. |
Cutting parameters of the experiments.
3.1. Numerical modeling
This work first involved the creation of the one-flute milling tool model and the cuboid workpiece model. The number of mesh elements on the workpiece was 95,052 and that on the milling tool was 194,116. The milling tool had 38,561 nodes and 22,152 surface polygons, illustrated in Figure 3, and an angular velocity of −100π rad/s (i.e., the tool rotates clockwise). The mesh of the shear zone between the milling tool and the workpiece is shown in Figure 4. This study defined a moving temperature boundary condition on the workpiece to simulate the translational and rotational motions of the laser beam spot with a radius of 0.7 mm and used several thermocouples to measure the surface temperature as a reference in FEA. More specifically, several boundary conditions were defined along the cutting path to simulate the movement of the laser spot. For example, the nodes in the entry area on the workpiece had an initial temperature of 850 °C, and other nodes further from the tool tip had an increasing temperature from the environment temperature to the pre-heating temperature. Each of these areas reached 850 °C at a certain step, and changes in the highest temperature spot showed movement of the laser shown in Figure 5. The center of the laser spot is 3 mm ahead of the milling cutter. The workpiece has a convection coefficient of 0.02 N/s mm °C with the environment, in which the temperature is 20 °C. Temperature distribution in the second experiment is shown in Figure 6. The simulation also included two mesh windows, which were defined on parts of the workpiece where the chip formed, the assumption being that the mesh windows would improve the accuracy of the results. Figure 4 shows that the mesh along the cutting path is finer. When the laser is on, the distribution of effective stress under 200 mm/min of the feed rate and 0.1 mm of the axial depth of milling is shown in Figure 7.
 |
Figure 3. Mesh of the milling tool. |
 |
Figure 4. Mesh of the shear zone between the milling tool and the workpiece. |
 |
Figure 5. Realization of moving heat source. |
 |
Figure 6. Temperature distribution of the shear zone in the second experiment (a) laser on (b) laser off. |
 |
Figure 7. Distribution of effective stress in the first experiment when the laser is on. |
3.2. Experimental setup
The experimental setup consisted of a 1000 W laser source and a water-cooling system, both of which were connected to the milling spindle, in which a TiSiN-coated tungsten carbide milling tool with a single flute was installed. The milling tool had a rake angle of 20.2°, a helix angle of 35°, and a 6 mm diameter with a 0.1 mm edge radius. As the same in the modeling, the laser beam spot has a radius of 0.7 mm. The center of the laser beam is 3 mm ahead of the milling tool, which can insure effective preheating effect. In the temperature measurement, the thermal couples are used. Since the laser locally heat the workpiece material, the milling tool cutting edge is very small area which we can assume that the temperature is information distributed near the cutting edge. The measurements are averaged to 850 °C. The measurement system included a four-component dynamometer (Kistler: Type-9272), a dynamometer amplifier (Kistler: Type-5019A), a triaxial accelerometer (Kistler: Type-8763-BB), an accelerometer amplifier (Kistler: Type-5070), and a data acquisition module (National Instrument: USB DAQ-6212). During laser-assisted end milling, forces in three directions were recorded for the first 10 s. The force signals between 1.5 s and 1.85 s from three experiments are shown in Figure 8. All the signals were periodic with two or three peak values in one period. While the highest wave magnitude occurred during the first one-fourth of the period since it was half slot milling, the second or third wave was the result of noise signals and chatter. During each period, the shapes of the force signals were almost the same, but the overall trend changed in some cases. During the third experiment, Fy moved to the positive direction, Fz moved slightly downward. These two trends, however, could not be accurately represented by the comparison of forces during only one period. Therefore, 30 periods were evenly selected from data collected in 10-s intervals and averaged for the calculation of forces. In addition, as the flat and second or third wave signals were unnecessary, only the forces measured within ±40% of the biggest peak were averaged, shown in Figure 9. Since the simulation in DEFORM did not last a complete revolution, the force signals collected between −40% to the peak values were averaged for comparison.
 |
Figure 8. Measured milling forces corresponding three milling conditions (a) a feed rate of 200 mm/min, an axial depth of milling of 0.1 mm (b) a feed rate of 200 mm/min, an axial depth of milling of 0.2 mm and (c) a feed rate of 300 mm/min, an axial depth of milling of 0.15 mm. |
 |
Figure 9. Schematic diagram for the average force calculation. |
4. Results
After collecting and averaging the force signals shown in Figure 8, the authors calculated the average force in three directions. DEFORM provided the option to track the contact forces between the tool and the workpiece through the simulation process. An example of recorded data for the third experiment under a laser is shown in Figure 10. For each simulation, the force in the X direction continued to increase, and the maximum force was recorded for almost all 500 steps. The force in the Y direction increased first and then decreased, and the maximum force appeared in the middle at about 375 steps. The force in the Z direction oscillated, but in general, it continued to increase, and the maximum force was recorded at about 500 steps.
 |
Figure 10. Contact forces in FEA for the third experiment when the laser is on. |
4.1. Comparison between FEA simulations and experimental measurements
The results of the simulations and the experiment as well as the error are listed in Table 4. From the measurements, this study concluded that the force in the x- direction was much greater than the other forces and the force in the feed direction was the smallest. When the axial depth of milling increased from the first to the second experiment, forces in both x- and y- directions increased accordingly. The combination of the increased axial depth of milling and the increased feed rate had similar effects in the first and third experiments. The results of the simulations were in close agreement with those of the experiment. The FEA showed the same trends in all three directions and matched in the feed direction, whose smallest error was about 5%.
Comparison between FEA simulations and experimental measurements.
4.2. Comparison between FEA simulations with and without a laser
To demonstrate the softening effect of a laser, this study also simulated the milling process under the same cutting parameters but without a laser. This study showed improvement in machinability in terms of decreased cutting forces. The average forces are listed in Table 5. All forces decreased when the laser pre-heating temperature was included. Softening was most effective in the axial direction since the largest drop in both the first and second experiments occurred in the Z direction. The force in the axial direction in the second experiment was more than 18% smaller when the Inconel 718 workpiece was softened. The laser also had more influence when the axial depth of milling increased from 0.1 mm to 0.2 mm. The percentage decreased from 0.58% to 1.53% in the cutting direction and from 2.97% to 18.08% in the axial direction. When the feed rate increased from 200 mm/min to 300 mm/min, and the axial depth of milling increased from 0.1 mm to 0.15 mm, the percentage decreased dramatically in the feed direction, from 1.69% to 7.11%. Figure 11 shows a comparison between forces in FEA with and without a laser for the second experiment.
 |
Figure 11. Comparisons between the forces in FEA with and without a laser for the second experiment in (a) x, (b) y, and (c) z directions; the horizontal axis indicates the time in μs, and the vertical axis indicates the forces in Newton. |
Comparison between FEA simulations with and without a laser.
5. Conclusions
In this study, the authors simulated the laser-assisted milling process on Inconel 718 in DEFORM. They simulated changes in material properties by including microstructure evolution and found that under the heating temperature of laser-assisted milling, Inconel 718 exhibits microstructure evolution in terms of grain growth in DRX. This study applied a strain- and temperature-induced recrystallization model that calculates the recrystallized volume fraction and captures grain growth, which reduces flow stress and lowers cutting forces in general. The authors selected three sets of cutting parameters under various feed rates and axial depths of milling and conducted three simulations as well as three experiments for validation. In addition, to show improvement in Inconel 718 machinability in laser-assisted milling, the study simulated the milling process under the same cutting parameters with the laser off. For FEA, this work applied a series of boundary conditions with varying temperatures to represent the movement of the laser spot. Each boundary condition contained an area with nodes, and the nodes in the entry area on the workpiece had an initial temperature of 850 °C while other nodes further from the tool tip underwent an increasing temperature from the environment temperature to the pre-heating temperature. The area in each boundary reached 850 °C at a certain step, and changes in the highest temperature spot represented movement of the laser. In addition, to improve the quality of the mesh, the study defined two mesh windows along the path of the milling tool, which obtained a much finer mesh. The simulation stopped at 500 steps when the rotation angle was 90°. Half-slot milling experiments were conducted on a single-beam coaxial laser-assisted milling spindle, which included 1000 W laser sources as well as a water-cooling system. This study collected periodic force signals in cutting, feed, and axial directions and averaged the measurements within ±40% of the maximum force in each period in the first 10 s.
By comparing the simulations and measurements from experiments, the authors found that the predicted values were in close agreement with measurements, particularly in the feed direction, in which the smallest error was around 5%. Two main reasons introduced big errors in certain cases. Chatter of the workstation introduced the error to experimental measurements, and the effect of the laser was simplified to a constant preheating temperature instead of a temperature or heat flux field. The Schematic diagram of half-slot milling in Figure 1 showed that the y-direction was the main cutting direction in this study, and the error in this direction was much smaller than the other two. So the simulation provided a better result in the main cutting direction. When the laser was off, this model predicted an increase in forces in all cases, which proved the softening effect of laser-assisted milling. The softening effect of laser was highly dependent on the axial depth of milling and feed rate, and the influence of laser varied in each case and cutting direction. In addition, when the axial depth of milling increased, the laser had a more significant influence, especially in the axial direction, in which the force with the laser was more than 18% smaller than that without the laser. This finding also matched the finding of Shi et al. [5]. Overall, by predicting the cutting forces in FEA, this study validated the influence of laser-assisted milling on Inconel 718.
References
- B.Z. XueFeng Wu, G.C. Feng, Thermal and cutting process simulation analysis of laser assisted milling of Inconel 718, in: Joint International Mechanical, Electronic and Information Technology Conference 2015. [Google Scholar]
- A. Devillez, et al., Cutting forces and wear in dry machining of Inconel 718 with coated carbide tools, Wear 262 (2007) 931–942. [CrossRef] [Google Scholar]
- Z. Pan, et al., Force modeling of Inconel 718 laser-assisted end milling under recrystallization effects, The International Journal of Advanced Manufacturing Technology (2017), DOI: 10.1007/s00170-017-0379-x. [Google Scholar]
- Z. Pan, et al., Analytical model for force prediction in laser-assisted milling of IN718, The International Journal of Advanced Manufacturing Technology (2016), DOI: 10.1007/s00170-016-9629-6. [Google Scholar]
- B. Shi, et al., Numerical and experimental investigation of laser-assisted machining of Inconel 718, Machining Science and Technology 12 (2008) 498–513. [CrossRef] [Google Scholar]
- K.Y. Nyon, et al., Finite element analysis of laser inert gas cutting on Inconel 718, The International Journal of Advanced Manufacturing Technology 60 (2011) 995–1007. [CrossRef] [Google Scholar]
- G. Wasle, B. Buchmayr, C. Lind, C. Sommitsch, FEM-coupled simulation of microstructure during hot forming processes, https://online.unileoben.ac.at/mu_online/voe_main2.getVollText?pDocumentNr=6519&pCurrPk=8222. [Google Scholar]
- E.A. Rahim, N.M. Warap, Z. Mohid, M.R. Ibrahim, N. Rafai, Numerical analysis of laser preheating for laser assisted micro milling of Inconel 718, Applied Mechanics and Materials 773–774 (2015) 332–336. [CrossRef] [Google Scholar]
- M.A. Balbaa, M.N.A. Nasr, Prediction of residual stresses after laser-assisted machining of Inconel 718 using SPH, Procedia CIRP 31 (2015) 19–23. [CrossRef] [Google Scholar]
- H. Ding, Microstructural prediction in metal cutting and improvement of machinability and surface integrity via laser-assisted machining, Purdue University, 2012. [Google Scholar]
- X.-M. Chen, et al., Dynamic recrystallization behavior of a typical nickel-based superalloy during hot deformation, Materials & Design 57 (2014) 568–577. [CrossRef] [Google Scholar]
- A. Reshetov, O. Bylya, N. Stefani, M. Rosochowska, P. Blackwell, An approach to microstructure modelling in nickel based superalloys, in: M. Hardy, E. Huron, U. Glatzel, B. Griffin, B. Lewis, C. Rae, V. Seetharaman, S. Ti (Eds.), TMS 13th International Symposium on Superalloys, Seven Springs (Pennsylvania), 2016, pp. 531–538. [Google Scholar]
- Z. Pan, S.Y. Liang, H. Garmestani, D.S. Shih, Prediction of machining-induced phase transformation and grain growth of Ti-6Al-4 V alloy, The International Journal of Advanced Manufacturing Technology 87 (2016) 859–866. [CrossRef] [Google Scholar]
- Z. Pan, et al., Modeling of Ti-6Al-4 V machining force considering material microstructure evolution, The International Journal of Advanced Manufacturing Technology (2017), DOI: 10.1007/s00170-016-9964-7. [Google Scholar]
- Z. Pan, A. Tabei, D.S. Shih, H. Garmestani, S.Y. Liang, The effects of dynamic evolution of microstructure on machining forces, Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture (2017), DOI: 10.1177/0954405417703430. [Google Scholar]
- D. Huang, W.T. Wu, D. Lambert, S.L. Semiatin, Computer simulation of microstructure evolution during hot forging of waspaloy and nickel alloy 718, in: R. Srinivasan, S.L. Semiatin, A. Beaudoin, S. Fox, Z. Jin (Eds.), Proceedings of Symposium: Microstructure Modeling and Prediction During Thermomechanical Processing, Indianapolis, November 4–8, TMS, Warrendale, 2001, pp. 137–146. [Google Scholar]
- L.A. Reyes, P. Páramo, A. Salas Zamarripa, M. de la Garza, M.P. Guerrero-Mata, Influence of processing parameters on grain size evolution of a forged superalloy, Journal of Materials Engineering and Performance 25 (2016) 179–187. [CrossRef] [Google Scholar]
- A. Loyda, G.M. Hernández-Muñoz, L.A. Reyes, P. Zambrano-Robledo, Microstructure modeling of a Ni-Fe-based superalloy during the rotary forging process, Journal of Materials Engineering and Performance 25 (2016) 2128–2137. [CrossRef] [Google Scholar]
- P.J. Arrazola, et al., On the machining induced residual stresses in IN718 nickel-based alloy: experiments and predictions with finite element simulation, Simulation Modelling Practice and Theory 41 (2014) 87–103. [CrossRef] [Google Scholar]
Cite this article as: Pan Z, Feng Y, Lu Y-T, Lin Y-F, Hung T-P, Hsu F-C, Lin C-F, Lu Y-C & Liang SY: Microstructure-sensitive flow stress modeling for force prediction in laser assisted milling of Inconel 718. Manufacturing Rev. 2017, 4, 6.
All Tables
All Figures
 |
Figure 1. Schematic diagram of half-slot milling, the cross indicates the instantaneous center location of a laser with a radius of 0.7 mm. |
| In the text | |
 |
Figure 2. Experimental setup of the single beam coaxial laser-assisted milling spindle. |
| In the text | |
 |
Figure 3. Mesh of the milling tool. |
| In the text | |
 |
Figure 4. Mesh of the shear zone between the milling tool and the workpiece. |
| In the text | |
 |
Figure 5. Realization of moving heat source. |
| In the text | |
 |
Figure 6. Temperature distribution of the shear zone in the second experiment (a) laser on (b) laser off. |
| In the text | |
 |
Figure 7. Distribution of effective stress in the first experiment when the laser is on. |
| In the text | |
 |
Figure 8. Measured milling forces corresponding three milling conditions (a) a feed rate of 200 mm/min, an axial depth of milling of 0.1 mm (b) a feed rate of 200 mm/min, an axial depth of milling of 0.2 mm and (c) a feed rate of 300 mm/min, an axial depth of milling of 0.15 mm. |
| In the text | |
 |
Figure 9. Schematic diagram for the average force calculation. |
| In the text | |
 |
Figure 10. Contact forces in FEA for the third experiment when the laser is on. |
| In the text | |
 |
Figure 11. Comparisons between the forces in FEA with and without a laser for the second experiment in (a) x, (b) y, and (c) z directions; the horizontal axis indicates the time in μs, and the vertical axis indicates the forces in Newton. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


