| Issue |
Manufacturing Rev.
Volume 8, 2021
|
|
|---|---|---|
| Article Number | 3 | |
| Number of page(s) | 23 | |
| DOI | https://doi.org/10.1051/mfreview/2021003 | |
| Published online | 10 February 2021 | |
Review
Micro milling process modeling: a review
College of Engineering and Technology, American University of the Middle East, Kuwait
* e-mail: ali.mamedov@aum.edu.kw
Received:
23
September
2020
Accepted:
20
January
2021
The trend towards miniature manufacturing in high technological fields like bioengineering, electronics and aerospace has increased dramatically over the last decade. Many methods of micro manufacturing have been researched and applied to manufacture small scale components. Among these manufacturing methods micro-mechanical machining methods have shown themselves to be attractive alternatives. Micro milling is one of the most frequently used micro-mechanical machining method with high potential for the precise manufacturing of complex parts. The aim of this work is to present the principal aspects related to micro milling technology, with emphasis on process modeling and quality of the finished product. A general view on process modeling starting from chip thickness models up to tool and workpiece machining induced distortion models is depicted. Specifically, different modeling techniques related to modeling of micro milling process are evaluated and important aspects that authors revealed during their research are presented. Finally, implications are discussed and suggestions for future research are presented.
Key words: Micro milling / system modeling / force modeling / tool deflection modeling / temperature modeling / distortion modeling
© A. Mamedov, Published by EDP Sciences 2021
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Micro milling is widely used in high-tech industries such as biomedical, aerospace, optics, electronics and die-mold with the increasing demand for precisely manufactured miniature parts. These industries have a high demand for tight manufacturing tolerances and surface quality. Additionally, they have complex geometries, which require micron level accuracy.
The demand for smaller and durable components with high number of functions has imposed strong requirements on manufacturing processes. The production of ultra-precise micro components for engineering products has become of value with recent advances in manufacturing field. In the same vein, ultra-precise manufacturing requires understanding of the fundamentals of micro cutting process such as chip formation, kinematics, dynamics, thermal aspects and surface integrity. Accordingly, researchers work on the causes and correlates of these fundamentals in order to understand how they differ from macro scale machining.
The purpose of this study is to shed light on different modeling approaches used to model mechanical and thermal aspects of micro milling in order to increase the efficiency of the process. Drawing on the literature, different force models are evaluated and compared. Results documented that the accurate estimation of forces is a critical point and it serves as the main input for thermal modeling of the process, tool deflection and workpiece distortion modeling.
2 Materials and methods
2.1 Chip thickness modeling
Previous research showed that micro milling is not exactly the scaled down version of conventional milling. Indeed, it differs from conventional milling in several aspects such as chip thickness, critical depth of cut, the cutting mechanisms, etc. Accordingly, understanding chip formation during micro milling is important for accurate force prediction. Kim et al. [1] reported that chip formation in micro machining differs from conventional machining. Unlike macro scale machining, a sharp cutting edge model is not valid for micro milling as chips occur along the rounded tool edge. Since, feed per tooth is higher than tool edge radius in conventional machining, the material is assumed to be removed by a sharp edge. However, due to small feedrate, depth of cut and relatively high tool edge radius in micro milling a large negative rake angle is formed, which cause elastic recovery of the workpiece material and rough surface. This phenomenon is defined as ploughing. Lucca et al. [2] stated that ploughing mechanism is more dominant than cutting mechanism when undeformed chip thickness is in the range of cutting edge radius. Liu et al. [3] analyzed minimum chip thickness from experimentally measured cutting forces and related a sudden change in thrust force to shift from ploughing to shear dominant cutting regime. Following that, Son et al. [4] investigated the effect of friction coefficient on minimum chip thickness and analytically formulated minimum chip thickness, in relation to the tool edge radius and friction coefficient of workpiece material. Vogler et al. [5] investigated minimum chip thickness for micro milling of steel by finite element model and reported that it differs between 20% and 35% of tool edge radius for different phase steels. They concluded that an accuracy of cutting force estimations is very much dependent on the accuracy of the chip thickness model. Henceforth, it is widely acknowledged to integrate the most accurate chip thickness model into micro milling mechanics models the estimation of cutting forces.
There are different chip thickness models available in the literature, which are developed from various kinematic analyses of micro milling process. Such models were derived from the fact that micro milling requires higher feed per tooth to tool radius ratios. Moreover it differs from conventional milling. It is noteworthy that the integration of different chip thickness models in the micro milling mechanics model will result in differences in the predicted cutting forces.
The chip thickness model presented by Martellotti [6] is the oldest and the most widely used model in the literature, especially for modeling conventional milling operations. In his study, Martellotti presented that the milling cutter follows a trochoidal path. This model assumes that the toolpath is circular, tool and machine geometries are ideal. In the most of conventional milling operations feed per tooth to tool radius ratio is small. Regarding that, model presented by Martellotti yields valid results and that they are widely used. Martellotti formulated his chip thickness model as following: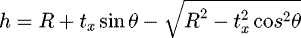 (1)where R is cutter radius, t
x
is feed per tooth and θ is immersion angle. However, the equation given above is approximated for cutting process with small t
x
/R ratio and is employed for the most of conventional milling processes as:
(1)where R is cutter radius, t
x
is feed per tooth and θ is immersion angle. However, the equation given above is approximated for cutting process with small t
x
/R ratio and is employed for the most of conventional milling processes as: (2)
(2)
Several researchers stated that traditional model cannot satisfy the accuracy demands of micro milling because of the simplifications made during the analyses. More specifically, these simplifications cause an error during the solution and that the presented model becomes no longer valid for high feed per tooth to tool radius ratios.
Bao [7,8] developed a chip thickness model for trochoidal tool path, considering the nature of chip thickness formation in micro milling at high feed per tooth to tool radius ratios and a trochoidal motion of the tool and tool run-out for suitable micro milling cutting conditions. The obtained chip thickness model is presented below in equation (3). (3)where R is cutter radius, t
x
is feed per tooth, N is number of cutting edges and θ is immersion angle. The physical meaning of each term in equation (3) is as following: the first term in the equation is a major contributor to the chip thickness, the second term is the difference between up and down milling and the third term is the additional chip thickness. Bao stated that an additional chip thickness term is important in micro milling simulations, because it calculates chip thickness at immersion angles close to 0 or 180°.
(3)where R is cutter radius, t
x
is feed per tooth, N is number of cutting edges and θ is immersion angle. The physical meaning of each term in equation (3) is as following: the first term in the equation is a major contributor to the chip thickness, the second term is the difference between up and down milling and the third term is the additional chip thickness. Bao stated that an additional chip thickness term is important in micro milling simulations, because it calculates chip thickness at immersion angles close to 0 or 180°.
Following that, Li et al. [9,10] proposed a numerical chip thickness model, with and without run-out. Researchers presented a chip thickness model, which uses true tool path. Wherein this model, they calculated undeformed chip thickness by finding the intersection point of the path curve left by the previous tooth and the line passing through the current tooth tip, as well as the cutter axis. The closed-form of the chip thickness proposed by Li is given below in equation (4), where R is cutter radius, t
x
is feed per tooth, N is number of cutting edges and θ is immersion angle.
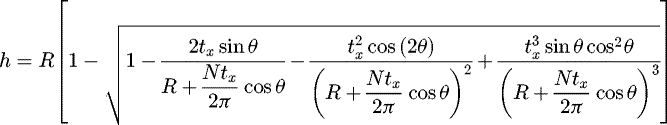 (4)
(4)
Kang and Zheng [11] developed a chip thickness model that sums conventional chip component with additional chip component and is expressed in terms of Fourier series. Researchers stated that in the expanded Martellotti's model estimation accuracy increases, while cutting flute approaches π/2 angular position and they have extended the expanded Martellotti's model to micro milling by calculating true chip thickness between two consecutive cutting paths. This model is expressed in terms of Fourier series and closed form of the model is demonstrated in equation (5), where R is cutter radius, t
x
is feed per tooth, N is number of cutting edges and θ is immersion angle. (5)
(5)
The available chip thickness models for micro milling are based on certain assumptions in the kinematic analysis, which results in differences in the simulated cutting force amplitudes. Mamedov and Lazoglu [12] presented comparative evaluation of chip thickness models for micro milling by examining their direct effects on the prediction of cutting forces. The root mean square deviation (RMSD) and the coefficient of determination (R2) values between the estimated and measured micro milling forces used for the comparative evaluation of all the chip thickness models at various feed per tooth to tool diameter ratios. Results showed that the chip thickness model developed by Li has the least root mean square deviation (RMSD) and the highest coefficient of determination (R2), which denotes that this model has better fit along with the experimental results. Another important finding made is that for the feed per tooth to tool diameter ratio smaller than 0.3, the RMSD values of all models are close to each other. However, for the feed per tooth to tool diameter ratio greater than 0.3, the effects of the chip thickness models in the force model are becoming more significant.
2.2 Force modeling
Many researchers investigated modeling of the micro milling forces in order to improve machining quality and understand nature of the process. Drawing on the results of previous studies, it is now more obvious that micro milling is different from conventional machining operations. Besides scaling down of the process, the presence of specific phenomena were brought on the scene. Kim et al. [1] calculated the difference between conventional and micro milling analytically.
Jin and Altintas [13] developed a finite element model for orthogonal cutting operation. Researchers presented a model, which is a function of chip area and cutting force coefficients. The model estimates cutting forces considering chip size, tool edge radius effect, tool run-out and dynamometer dynamics. Based on the estimated cutting forces cutting coefficients are expressed as a non-linear function of tool edge radius and uncut chip thickness as demonstrated in equation (6). (6)
(6)
Here, terms  describe force components when edge radius is zero and terms
describe force components when edge radius is zero and terms  describe nonlinear effect of tool edge radius on cutting forces, h is uncut chip thickness, r is tool edge radius and α, β, d, p, q are coefficients calculated from FE simulations. The model takes strain rate and strain hardening into account, as well as temperature effects. In addition, researchers underlined that, while measuring periodic cutting forces in micro-milling process the frequency bandwidth of dynamometer is inadequate due to the high spindle speeds. When the tooth passing frequency of the force signal is beyond the bandwidth of the dynamometer, the force measurement is distorted with regard to the structural mode of the measurement system. In order to compensate the dynamics of force sensor system authors implemented Kalman filter, as proposed by Altintas and Park [14]. The result of modeled forces and implemented filter is demonstrated in Figure 1.
describe nonlinear effect of tool edge radius on cutting forces, h is uncut chip thickness, r is tool edge radius and α, β, d, p, q are coefficients calculated from FE simulations. The model takes strain rate and strain hardening into account, as well as temperature effects. In addition, researchers underlined that, while measuring periodic cutting forces in micro-milling process the frequency bandwidth of dynamometer is inadequate due to the high spindle speeds. When the tooth passing frequency of the force signal is beyond the bandwidth of the dynamometer, the force measurement is distorted with regard to the structural mode of the measurement system. In order to compensate the dynamics of force sensor system authors implemented Kalman filter, as proposed by Altintas and Park [14]. The result of modeled forces and implemented filter is demonstrated in Figure 1.
Park and Malekian [15] developed a cutting force model that considers cutting forces generated by shearing and ploughing mechanisms. Cutting forces generated by shearing mechanism are formulated similarly to conventional milling and expressed in form of shearing and edge coefficients as shown in equation (7): (7)
(7)
Whereas, cutting forces generated by ploughing mechanism are formulated as a function of ploughed volume as shown in equation (8):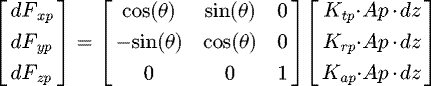 (8)where dFxs
, dFys
and dFzs
represent shearing components of differential x, y and z forces, dFxp
, dFyp
and dFzp
represent ploughing components of differential x, y and z forces, Ktc
, Krc
and Kac
are cutting coefficients, Kte
, Kre
and Kae
are edge coefficients, Ktp
, Krp
, Kap
stand for ploughing coefficients, dz denotes differential axial depth of cut, h stands for uncut chip thickness and Ap denotes ploughed area, which depends on height of elastically recovered material, edge radius of the tool and clearance angle.
(8)where dFxs
, dFys
and dFzs
represent shearing components of differential x, y and z forces, dFxp
, dFyp
and dFzp
represent ploughing components of differential x, y and z forces, Ktc
, Krc
and Kac
are cutting coefficients, Kte
, Kre
and Kae
are edge coefficients, Ktp
, Krp
, Kap
stand for ploughing coefficients, dz denotes differential axial depth of cut, h stands for uncut chip thickness and Ap denotes ploughed area, which depends on height of elastically recovered material, edge radius of the tool and clearance angle.
Later, Mamedov and Lazoglu [16] used similar approach to simulate cutting forces for micro ball-milling of freeform workpiece. Researchers used feedrate scheduling technique to improve machining performance during roughing operation. The cutter-workpiece engagement was calculated at each cutter location (CL) point to estimate the entrance and exit angles of each discrete cutting disc. Based on calculated engagement, resultant cutting force kept constant at desired value for all cutter location (CL) points by alternating feedrate. Instant feedrate for each cutter location point was calculated with formulation shown in equation (9), where F
1,i
is an estimated resultant force at point i for feed f
1 and F
2,i
for feed f
2 ⋅ F
lim,i
is a threshold value of resultant cutting force for i
th
CL point. Experimental validations showed that proposed techniques reduce roughing operation time by two times. (9)
(9)
Malekian et al. [17] investigated dynamics of micro milling process. Researchers revealed that receptance coupling of the machining center, spindle and micro tool should be considered for accurate modeling of micro milling operation. Additionally, the rotational dynamics of the substructures should be included in simulations. Therefore, dynamics of micro milling tool is obtained from FE analysis and dynamics of spindle is determined through experimental modal analysis. Presented receptance coupling method allows predicting overall assembled system dynamics and its effect on uncut chip thickness and cutting force variations.
Jun et al. [18] developed a model for micro milling that predicts dynamic cutting forces and micro end mill vibrations. The model employs chip thickness configuration that considers the elastic-plastic nature of the ploughing/rubbing and elastic recovery. The spring back of the surface due to elastic recovery is formulated as: (10)Which means that only elastic deformation occurs in the workpiece material when the uncut chip thickness h is smaller than a certain critical value h
e
. As h increases beyond h
e
, the deformation becomes mixed elastic-plastic. In this case, a constant percentage p
e
of the workpiece material undergoes elastic recovery as the tool passes. The other material undergoes plastic deformation. Finally, when h increases to the minimum chip thickness, denoted as h
min
, the deformed material is removed as a chip and the elastic recovery rate drops to 0.
(10)Which means that only elastic deformation occurs in the workpiece material when the uncut chip thickness h is smaller than a certain critical value h
e
. As h increases beyond h
e
, the deformation becomes mixed elastic-plastic. In this case, a constant percentage p
e
of the workpiece material undergoes elastic recovery as the tool passes. The other material undergoes plastic deformation. Finally, when h increases to the minimum chip thickness, denoted as h
min
, the deformed material is removed as a chip and the elastic recovery rate drops to 0.
Fang et al. [19,20] performed a more detailed study on plasticity model and investigated elastic recovery of ploughed material. Researchers utilized a slip-line field model to estimate shearing and ploughing forces. The presented model consists of slip-line sub-regions, as demonstrated in Figure 2, each having its own physical meaning. The model accounts for the effects like shear zone effect, size effect and chip up-curl radius.
Jing et al. [21] proposed a hybrid force model for predicting cutting forces during micro end milling. The cutting force coefficients are obtained from finite element model of orthogonal micro cutting and then integrated into mechanistic force model, introduced by Altintas [22], which can predict cutting forces for required cutting conditions. Numerically calculated cutting force coefficients are expressed as nonlinear functions of cutting speed and uncut chip thickness. Jing et al. [23], also proposed a hybrid model to estimate cutting forces during micro milling operation through determination of instantaneous uncut chip thickness that considers the combination of the minimum chip thickness, tool run-out, and the material's elastic recovery.
Recently, Zhang et al. [24] presented a generic instantaneous force model for micro milling, which includes the size effect in the force coefficients and the tool runout effect in the instantaneous uncut chip thickness. The real engagement is identified under the tool run out effect, the average uncut chip thickness, actual cutting depth, center position and geometrical relations are analytically established. This leads to better adaptability and eases process modeling and online control.
 |
Fig. 1 Comparison of cutting forces and the frequency spectrums at: n = 10 000 rpm, c = 3 µm/tooth, a = 50 µm [13]. |
 |
Fig. 2 The division of slip-line field. (a) Three major shear zones. (b) A total of 27 slip-line sub regions [19]. |
2.3 Tool deflection and surface roughness modeling
Cutting forces during micro milling process result in tool deflection and form error of machined surface. Many researchers have worked on modeling of tool deflections during conventional milling operation in order to improve the quality of final machined parts.
Tool deflection of micro end-mill was modeled by Mamedov et al. [25], who, unlikely from previously developed conventional models, proposed to consider cutting forces as distributed loads along cutting flutes in the workpiece tool contact zone. The tool is considered as a cantilever beam supported in the tool holder and modeled as a cylinder with variable cross sections. Also, tool is sliced into disks with discrete thickness and forces estimated by force model are applied on each the disk at certain cutter locations. The tool is modeled as a two-dimensional Timoshenko beam element. Stiffness matrix of an element (Ke
) is calculated as shown in equation (11):
 (11)
(11)
 (12)
(12)
Above, L is the element length, E is modulus of elasticity, G is shear modulus, A is cross section area and I is moment of inertia. Later, element matrices are assembled to the structure stiffness matrix K and tool deflections are calculated from equation (13), where F
x
and F
y
are respectively cutting forces vectors in x and y direction.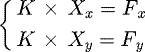 (13)
(13)
Proposed model was validated on Titanium alloy Ti-6Al-4V using 800 μm diameter two fluted Tungsten Carbide micro end mill on Mori Seiki NMV5000 DCG 5-axis CNC milling machine and micro end-mill deflections measured by two laser displacement sensors. Deflection estimation and experimentally measured results are presented Figure 3.
Sun et al. [26] worked on modeling on surface generation process. Researchers revealed that chip thickness fluctuations result in highly non-uniform surface. To estimate generated surface authors proposed the relative standard deviation of surface roughness (RSDS) method. This method considers minimum chip thickness effect, alignment errors, relative tool sharpness, material elastic recovery and ploughing. The algorithm shown in Figure 4 explains working principle of the developed surface generation model. Where, discrete surface roughness is the sum of geometric surface roughness and stochastic surface roughness. The geometric surface roughness is derived through calculating the value of tool residual marks and its corresponding elastic recovery height in the feed direction. Tool residual marks are formed by the superposition between previous surface profile and tool edge profile, which is determined by instantaneous uncut chip thickness between two neighboring tool trajectories. Whereas, stochastic surface roughness is a function of special cutting mechanisms such as ploughing effect and minimum chip thickness effect. It is acquired through calculating the normal specific ploughing amount (NSPA) that is defined as the arithmetic product between the ratio of the volume of ploughed material to the volume of total tool-workpiece contact material and the normal vector of chip flow, as shown in equation (14): (14)where, A
t
is the total volume of tool-workpiece contact material, γ is the rake angle and A
s
and A
p
represents the volume of sheared material and ploughed material, respectively. The 3D topographies of the finished surfaces and surface roughness in the feed direction were acquired through employing an optical surface microscope and scanning electron microscope as shown in Figure 5. Results of the simulations and experimental measurements revealed that the cutting speed has no apparent connection with surface uniformity, but both feed rate and depth of cut have a pronounced influence on surface uniformity.
(14)where, A
t
is the total volume of tool-workpiece contact material, γ is the rake angle and A
s
and A
p
represents the volume of sheared material and ploughed material, respectively. The 3D topographies of the finished surfaces and surface roughness in the feed direction were acquired through employing an optical surface microscope and scanning electron microscope as shown in Figure 5. Results of the simulations and experimental measurements revealed that the cutting speed has no apparent connection with surface uniformity, but both feed rate and depth of cut have a pronounced influence on surface uniformity.
Leo Kumar [27] proposed an empirical model that employs regression modeling based on experimental data in order to characterize the relationship between independent and dependent variables, such as arithmetic average surface roughness, machining time, spindle speed and feedrate. Later, Genetic Algorithm based on the principle of natural genetics and natural selection was used to minimize surface roughness and machining time. As the result author concluded that combination of low spindle speed and feed rate yields good surface finish. As feed rate increases, surface quality gets decreased. Whereas, Aslantas et al. [28] stated that according to Analysis of Variance of results for surface roughness, depth of cut is the most influential parameter during micro milling of Ti-6Al-4V alloy.
Beruvides et al. [29] proposed real-time system capable of predicting surface roughness as a function of the z-axis vibration captured during the cutting process. System consists of mono-axial accelerometer on the z-axis, with a sensitivity of 10.58 mV/g and bandwidth of 20 kHz that is connected to an amplifier and data acquisition system. Artificial Intelligence techniques were used to overcome noise in vibration signal and to obtain a regression model with a good generalization capability. Also, Multiple Linear Regression technique was used to estimate surface roughness. The relationship between the dependent variable logarithm (surface roughness) and the logarithms of the independent variables (cutting speed, feedrate, and depth of cut) was employed to generate an exponential model. The z-axis vibrations are used as the main input of the model to predict average surface roughness.
Vipindas and Mathew [30] analyzed wear mechanisms during micro milling process and revealed the relation between cutting parameters, which have direct relation to cutting regimes, and surface roughness. Researchers performed wear tests on Ti-6Al-4V with micro end-mill at 15.7 m/min cutting speed at two different feedrates 5 and 0.3 μm/tooth. Results, presented in Figure 6, showed that with 5 μm/tooth feedrate, initially surface roughness decreases with machining length and reach a minimum value at ∼700 mm length of cut and then increases with machining length. Whereas with 0.3 μm/tooth feed rate, surface roughness increases continuously with machining length. This could be due to the fact that, initially shearing mechanism is predominant, when feedrate (5 μm/tooth) is greater than edge radius of the fresh tool (3–3.5 μm). As machining progresses tool edge radius increases due to wear and at one point exceeds feedrate. Here, mechanism is ploughing dominant and surface roughness of the machined surface starts to increase. Whereas in the second case, when feedrate (0.3 μm/tooth) is already smaller than edge radius of the fresh tool (3–3.5 μm) ploughing is dominant regime from the beginning of the cutting process. Therefore, as machining progresses tool edge radius increases due to wear, which results in increased ploughing, which in turn increases the surface roughness with machining length. This could be the reason for a continuous increase in surface roughness with machining length at 0.3 μm/tooth feedrate. Therefore, for the applications where surface roughness is important factor it is recommended to select a feed rate slightly higher than the tool edge radius.
Chen et al. [31] proposed a 3D surface generation model that accounts for regenerative effect of system dynamics, cutting process effects and cutter runout. Authors modeled the dynamic response of the machine tool system under the action of the cutting forces as was described by Altintas and Montgomery [32] and generated stability lobes of according to Schmitz and Smith [33] as shown in Figure 7. By using abovementioned inputs, authors generated 3D surface topography and validated it with several experimental results, as presented in Figure 8. Similarly, Chen et al. [34] developed the textured surface generation mechanism in vibration-assisted micro milling through modelling and experimental approaches. A surface generation model decouples the effects of tool geometry and kinematics of vibration-assisted milling. To accurately model the vibration-assisted milling surface generation process, the cutting edge detection and modelling, the kinemics modeling and analysis, and the coordinate transformation from cutting edge to workpiece surface are used. Authors use an HMT-based calculation algorithm for the surface generation. This algorithm initially detects the geometry of the cutting edge and discritize the cutting edge together with workpiece into series of points. Later, these points are transfered on the cutting edge from tool coordinate system to workpiece coordinate system. Finally, these points are plotted in the workpiece coordinate system to generate the final machined surface, as shown in Figure. 9.
Zhang et al. [35] presented an improved analytical surface generation model for micro milling that considers stochastic tool wear. The proposed surface generation model uses probabilistic approach based on the particle filter algorithm to predict the stochastic tool wear progression. The online measurement data of cutting forces and tool vibrations are also linked with the state of tool wear. The cutting edge trajectory for micro milling is determined by a theoretical and empirical coupled method, based on the process kinematics, tool run-out and stochastic tool wear. The proposed surface generation model is validated with milling experiments of Al6061 under various machining conditions. Generated surface is measured with a 3D surface profilometer and compared with predicted surface topograpthy, as shown in Figure 10.
Chen et al. [36], developed a novel 3D surface generation modelling method for micro milling, which considers the effect of machining non-linear dynamics. The relationship between machining process and surface topography is established considering the effects of machining process kinematics, tool run-out and the nonlinear dynamic regenerative effect of the machining system. Model is validated on three typical machining cases, static stable, dynamic stable and unstable machining.
Matsumara and Ono [37,38] analysed an influence of tool inclination on surface generation during micro ball end milling of glass. Authors pointed out that due to absence of elastic deformation in glass, the edge roughness of cutting tool is transferred directly onto the surface without elastic recovery. They presented an analytical model to discuss the surface profile in cutting with the ball end mill, which is inclined at the angle θ in the feed direction of the cutter. The presented model shows that the tool inclination compensates for deterioration of the surface finish induced by the edge roughness. Authors also estimate the maximum feedrate and feed directions at which brittle fracture does not occur. Results showed that the positive tilt angle results in high critical feed rates. When the tools are tilted at negative angles, the feed rate should be low to get the crack-free surfaces.
Liu et al. [39] presented the surface-generation models for the sidewall and floor surfaces generetad during micro end milling. In the sidewall surface-generation model, the deterministic model characterizes the surface topography generated from the relative motion between the major cutting edge and the workpiece material. In the floor surface-generation model, the deterministic model characterizes the three-dimensional surface topography over the entire floor surface and considers the effects of the minimum chip thickness, the elastic recovery, and the transverse vibration. Authors also point out that geometry of the micro end mill consists of macrogeometry and microgeometry. Macrogeometry is defined by nominal tool parameters, such as tool radius, flute number, helix angle, rake angle, clearance angle etc. While, microgeometry is the deviation of the cutting edge geometry from the ideal sharp tool. It is characterized by the geometric features along the cutting flutes, such as edge radius and edge serration.
Recently, Groß et al. [40] presented the surface generation model that uses several different techniques such as integral approach, correlation analysis and Fourier analysis in order to investigate surface topography details in a smaller order of magnitude. Evaluation results showed the correlation between surface texture parameters and machining parameters. Results revealed that kinematic substructures formed on generated surface are significantly influenced by the feed per tooth. While effects of material separation are strongly influenced by the selected spindle speed.
 |
Fig. 3 Simulated and experimental deflection values of the tool tip in x and y direction for depth of cut 100 μm and feedrate 5 μm/rev-tooth under down-milling cutting condition [25]. |
 |
Fig. 5 Finished surface characteristic and cross-sectional 2D profile with depth of cut at 10 µm and feed rate 0.8 µm/flute [26]. |
 |
Fig. 6 Surface roughness variation with tool wear with (a) 5 μm/tooth feed rate, (b) 0.3 μm/tooth feed rate [30]. |
 |
Fig. 8 Simulated surface at spindle speed of 80 000 rpm. (a) without considering the machining dynamics; (b) considering the machining dynamics; (c) experimental result [31]. |
 |
Fig. 10 Predicted and measured surface topography of micro milling process with spindle speed 20 000 rpm, feed rate 0.2 mm/ s, radial depth of cut 0.508 mm, and axial depth of cut 0.15 mm [35]. |
2.4 Thermal modeling
The temperature in micro machining of advanced engineering materials like Titanium alloys is one of the critical factors affecting an accuracy of parts. Thermal simulation of the micro machining is important since the heat generated during the metal cutting process directly affects material properties of the tool and the workpiece, deflection of the tool, geometrical tolerances and residual stresses produced in manufactured parts. Accordingly, modeling of temperature becomes essential for machining alloys with difficult thermo-mechanical properties like Ti-6Al-4V.
Komanduri and Hou [41–43] presented extensive work on temperature modeling during metal cutting. They have developed an analytical model that estimates temperature rise due to heat generated in the primary shear zone. Different from previous papers they modeled heat flow and temperature distribution in both workpiece material and chip. Later, in the second study they presented a model that estimates temperature distribution between tool and chip due to frictional heat source at tool-chip interface. And in the final part of their work authors presented a combined model with common coordinate system that estimates total temperature distribution due to shear and friction heat sources, as shown in Figure 11. Described model implements Hahn's moving oblique band heat source in primary shear zone and Jaeger's moving band heat source in tool-chip contact interface.
Lazoglu and Altintas [44] used finite difference method to model temperature for continuous and interrupted machining operations considering shear energy formed in the primary zone, friction energy created at the chip-tool interface and the heat balance between chip and cutting tool. The temperature field is modeled as first-order dynamic system and time constant is identified based on tool and workpiece material properties. Heat sources used in temperature simulations were calculated based on methodology earlier presented by Altintas [22], where heat generated in the primary deformation zone due to the shearing is estimated as a function of shearing force and shearing velocity. Whereas, heat generated in the secondary deformation zone is estimated as a function of chip velocity and friction force on the rake face. In the presented model the variation of the tool-chip transient contact temperature for continuous machining processes, such as turning, is determined by calculation of steady-state tool and chip temperatures, and time constant. Alternately, for interrupted machining process, such as milling, the variable chip thickness is discretized into constant sections and each section is considered like a continuous machining process for a discrete machining time.
Later, Lazoglu and Islam [45] developed a 3D temperature model for oblique machining operations. Finite difference method was used to solve heat transfer problems and a general oblique cutting process model was employed for the prediction of the temperatures of turning operation. The analytical approach that used elliptic structural grid generation to solve the temperature field allowed different cutter geometries to be implemented and the analytical nature of the model improved the computational time significantly.
Lin et al. [46] proposed a temperature model that considers heat generated due to flank rubbing. Since, authors are estimating only workpiece temperature they didn't include heat source at tool-chip interface, but different from previous studies they have added a heat source to a flank surface of the tool, in addition to shear plane heat source. Flank surface is the surface of the tool that has direct contact with the workpiece and in continuously increasing with progressive tool wear. Total heat in the flank surface is expressed as a product of fraction of flank wear surface heat conducted into workpiece and the heat flux of elemental flank surface heat source, which is presented as a function of cutting velocity, elemental tangential force component due to flank wear, tool flank wear width and elemental axial length. The heat transfer and heat partition used in the model are presented in Figure 12.
Yang et al. [47] have developed a thermo-mechanical finite element model of the micro milling process, where the flow stress of the material is expressed by Jonson − Cook constitutive equation, shown in equation (15), and transient temperature distribution is expressed by equation
(16), where A is the yield strength of the material at room temperature and  represents the plastic equivalent strain. The strain rate
represents the plastic equivalent strain. The strain rate  is normalized with a reference strain rate
is normalized with a reference strain rate  . T is the workpiece temperature, T
melt
and T
room
are the material melting and room temperatures, Q is the rate of specific volumetric heat flux, ρ is the material density and t is the time. Proposed model estimates the effect of tool edge radius on cutting force, effective stress and mean temperature for micro end milling of an Al2024-T6 alloy. Both simulated and measured with infrared camera temperature results showed that with an increase of tool edge radius, the cutting force increases, while the effective stress and mean cutting temperature of the micro-cutter decreases.
. T is the workpiece temperature, T
melt
and T
room
are the material melting and room temperatures, Q is the rate of specific volumetric heat flux, ρ is the material density and t is the time. Proposed model estimates the effect of tool edge radius on cutting force, effective stress and mean temperature for micro end milling of an Al2024-T6 alloy. Both simulated and measured with infrared camera temperature results showed that with an increase of tool edge radius, the cutting force increases, while the effective stress and mean cutting temperature of the micro-cutter decreases. (15)
(15)
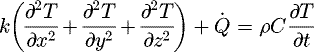 (16)
(16)
Wissmiller and Pfefferkorn [48] presented modeling and measurement techniques for temperature measurement and discussed cooling strategies for the micro milling process. A two-dimensional transient heat transfer model is employed for temperature estimations during the cutting process. Authors modeled heat input as a uniform heat flux and mentioned that even if the heat distribution is non-uniform in reality it requires additional study of tool-chip-workpiece interaction, which is beyond the scope of their paper. Both numerical and experimental results showed that the tool temperatures increase with increasing feedrate, even if, the measurements at higher feedrates correspond to shorter machining times since the length of cut is held constant. Authors also proposed cooling strategies such as changing the tool design by reducing the flute length and transition length, which will increase thermal conductivity and decrease tool temperature. However, this method has limited application because such modification will simultaneously limit the depth of cut of the tool. Another proposed method is liquid nitrogen cooling of the tool. Since, the most dominant regime of the heat transfer in this particular case is conduction along the tool, authors proposed the heat removal by liquid nitrogen through the top of the tool. Even if, experimental results showed that heat is reduced compared to the case without cooling, this method has its own shortage − dimensional accuracy. With the application of the liquid nitrogen cutting tool undergoes thermal contraction, which is more significant in axial direction.
Mamedov and Lazoglu [49] developed a thermo-mechanical model of the micro milling process that overcomes the shortage of non-uniform heat distribution described in Wissmiller and Pfefferkorn's [48] paper. The proposed thermo-mechanical model calculates main heat inputs, generated in the primary and secondary deformation zones, as instantaneous heat sources in the shear plane and on the chip-tool contact surface. Heat inputs and contact areas are calculated instantaneously as a function of the immersion angle θ. Heat generated in the primary deformation zone due to the shearing, frictional power generated in the secondary deformation zone, the chip contact length and shear plane length are calculated as presented in equation (17)–(20), respectively [22], where P
f
is the friction power, P
s
is the shearing power, V is the cutting velocity, V
s
is the shearing velocity, V
c
is the chip velocity, F
s
is the shear force on shear plane, F
u
is the friction force on the rake face, F
R
is the planar resultant cutting force, τ
s
is the average shear flow stress, h is the uncut chip thickness, a is the rake angle, α
n
is the normal rake angle, φ
n is the normal shear angle, φ
c is a shear angle,
θ is the immersion angle and β
a
is the average friction angle. (17)
(17)
 (18)
(18)
 (19)
(19)
 (20)
(20)
Estimated shearing and frictional heat values are employed as the heat input sources to the shearing and frictional zones in the finite element thermal simulations of the micro milling, as shown in Figure 13.
Ozel et al. [50] investigated on effects of machining parameters on surface roughness and tool wear for uncoated and cBN coated micro tools. A finite element model is employed to predict cutting forces, temperatures and wear rate of uncoated and cBN coated tool. Simulation results reveal advantages of cBN coating. Due to a lower friction coefficient and higher effective thermal conductivity cBN coated tool has lowest temperature rise during machining of Ti-6Al-4V alloy.
 |
Fig. 11 Schematic of the heat transfer model with a common coordinate system for the combined effect of two principal heat sources: the shear plane heat source and the tool-chip interface frictional heat source [43]. |
2.5 System modeling
Chatter is a common problem in machining operations causing poor surface finish and damage to cutting tool. Chatter stability diagrams are frequently used to estimate favorable machining conditions. Different from conventional milling, the high rotational speeds of micro-milling cause changes in dynamics; and, the elastoplastic nature of micro-machining operations results in changes to the cutting coefficients. Variations in dynamics and cutting coefficients affect the stability lobes. One of the requirements for generating the stability diagrams is tool point frequency response function (FRF). Experimental modal analysis is the most common method of determining the tool point FRF [22]. However, due to their fragile structures, impact testing is not suitable for micro-milling tools. Therefore other methods must be utilized in order to obtain tool point FRFs of micro-milling tools.
Yilmaz et al. [51] presented an analytical model for tool point FRF of micro end mills. Authors used an inverse algorithm to correct geometric representation and damping of the tool. In the inverse stability approach the modal parameters in the FRF are the unknowns and the chatter frequency and depth of cut are the values obtained experimentally. The modal parameters can be identified by equating the experimentally obtained chatter frequency and corresponding axial depth of cut with their analytical definitions. Using the modal parameters a stability diagram is generated and it is verified with further chatter experiments. Then, the model parameters obtained from the experiments are used to update the analytical model to better represent the micro-end mill tool tip dynamics. Authors use an acoustic emission sensor and a microphone to record the sound throughout the process. Frequency content of the recorded sounds is inspected to determine the chatter frequency.
Park and Rahnama [52] developed a robust chatter stability theorem, which is based on the edge theorem, to provide the robust stability within the minimum and maximum boundaries of changing parameters. In conventional chatter stability theories, the cutting parameters are considered to be constant. However, some parameters, such as system dynamics and cutting coefficients, change during micro-milling operations. The robust chatter stability theorem, based on the edge theorem and the zero exclusion principle, is utilized to find stability within the changing boundaries. The edge theorem is an extension of Kharitonov's robust theory that allows us to predict the stability of an uncertain time-delay system, whose parameters vary within a certain range. To find the stability lobes for micro-milling operations, the algorithm sweeps the depths of cut and chatter frequencies at each spindle speed; and, it checks the stability through the proposed automated zero exclusion method. The first set of unstable conditions is recorded as the border between the stable and unstable regions, in order to determine the stability lobes. Authors used the receptance coupling (RC) method to obtain the dynamics at the tool tip. This method mathematically combines the results of experimental modal analysis (EMA) of the spindle and machine tool with the result of finite element analysis of the tool to come up with the overall dynamics at the tool tip. In previously published work Rahnama et al. [53] also modeled chatter stability in micro end milling while considering the effect of process damping. Process damping of micro milling has been modeled by identifying the elastically deformed area under the tool tip. The process damping coefficient, which was obtained experimentally during micro end milling tests in ploughing dominant regime, is a function of waves left on the surface due to the tool movement on the workpiece, tool geometry and cutting conditions, such as chip thickness, clearance and effective rake angles.
Later, Graham et al. [54] evaluated two different methods for prediction of chatter stability in micro milling, namely Edge theorem and Linear Matrix Inequality (LMI) method based on Lyapunov stability theory. They also compared both methods with analytical chatter stability model. The Edge theorem approach is applicable only for time invariant uncertain systems in the frequency domain. In reality, many systems are time varying in nature and alternative robust control theories are needed to describe uncertain systems more generally. Based on Lyapunov stability theory, LMIs can be used to describe stability conditions for both time invariant and time varying uncertain systems and establish robust stability. As shown in Figure 14, while machining is guaranteed to be stable below robust stability lobes, stable machining conditions may still be available at points above the predicted robust limits. However, unstable points were detected below the lobes predicted by the analytical chatter stability model, whereas the robust methods give a more conservative cutting depth prediction. In comparison to the Edge theorem approach, LMI methods require increased computational effort.
Singh and Singh [55] proposed a receptance coupling method to estimate the micro-end mill dynamics. Similar to methodology proposed by Park and Rahnama [52] it combines the frequency response functions for the two substructures (machine tool with a portion of shank and the micro-end mill) to determine the tool-tip dynamics. However, authors pointed out that there are certain issues with the receptance coupling which uses only two locations for determining the FRF one at the coupling and other at tip unlike the component mode synthesis, which allows use of mode shapes at multiple points in the substructures. Therefore, the component mode synthesis approach has been used to couple the substructures. The mode synthesis approach adopted in this work contains the position dependent modes along the length of substructures. The mode shapes of machine-tool shank substructure are determined experimentally whereas the micro-end mill mode shapes are determined via finite element method (FEM). The presented approach has been analysed for two different cases: (a) idealized micro end mill by assuming a micro end mill as a cantilevered Timoshenko beam, (b) considering micro end mill with machine tool compliance, as shown in Figure 15.
Mokhtari et al. [56] used a 3-D nonlinear dynamic model of the micromilling tool including non-uniform geometry, structural nonlinearity, gyroscopic moment, rotary inertia, process damping, and size effect to investigate chatter phenomenon in micro milling. The cutting tool has been modeled as a rotating non-uniform clamped free Timoshenko beam which is excited by cutting forces. The complete system governing equations have been achieved for three dimension lateral beam vibrations. The method of multiple scales has been employed to find analytical solution for delay nonlinear partial differential equations of motion. The presented work investigates effects of the axial depth of cut, the gyroscopic moments, rotary inertia, the process damping, the size effect, the number of the cutter tooth, the tool length, and the tool diameter on the chatter boundary. As the result, authors pointed out that neglecting size effects, gyroscopic moments, and rotary inertia in the tool model causes significant errors in prediction of the stability boundary of the process. Increasing the number of tool flutes may stretch out of the lobes and decrease number of lobes. Finally, increasing the diameter of fluted section, decreasing the length of this part, and considering size effect in the tool model increase the stability of the micro-milling tool.
 |
Fig. 14 Comparison of robust stability lobes with analytical stability lobes and experimental chatter points [54]. |
2.6 Machining induced distortion and residual stress modeling
Manufacturing of parts within tight tolerances is becoming more and more essential. Distortions are one of the major concerns when manufacturing parts that have small cross sections, like thin walls. Due to this reason, it is crucial to predict distortions of the thin wall and develop strategies to prevent geometrical errors. In order to develop a model that simulates machining-induced distortions, it is necessary to have a clear understanding of mechanics and thermal aspects of the cutting process. Several groups of researchers worked on modeling of the cutting forces, temperature, residual stresses and surface integrity that affect machining-induced distortions.
Jawahir et al. [57] published a comprehensive work on recent progress in experimental and theoretical investigations of residual stresses, where they investigated and compared main residual stress modeling techniques available in the literature. Authors also mentioned available techniques, such as diffraction based methods, micro magnetic methods and acoustic methods, used for measuring machining induced residual stresses. The basic principle of diffraction based methods relies on the measurement of inter planar atomic spacing and elastic strains in surfaces when subjected to an applied or internal stress from which the residual stress can be determined [58]. The measuring principle of micro magnetic methods is based on the influence of residual stress and hardness values and the structure of subsurface layers on the magnetic domains of ferromagnetic materials [59]. Finally, the basic principle of acoustic methods relies on the generation and propagation of acoustic waves affected by various material parameters such as elastic, thermal, electric and magnetic properties [60].
Denkena et al. [61] investigated the effect of cutting parameters on residual stresses and subsurface material changes in Aluminum alloys. Due to the high cutting speed requirement of the material, structural components manufactured from Aluminum are machined at high cutting speeds and feedrates, which results in formation of high thermo-mechanical loads and residual stresses. Authors analyzed the effect of several parameters on the residual stress starting from cutting speed. From the experiments it was seen that the increase of the cutting speed may reduce the compressive residual stresses on the surface, but this is valid for certain range only. After a while residual stress remains approximately constant. It was also noted that variation of the cutting speed does not systematically influence the depth of the maximum residual stresses. On the other hand, the effect of feedrate on the residual stresses is more significant. The residual stress at the surface tends to be less compressive or to a zero value with the increase of the feedrate, while the maximum compressive residual stress significantly increases. This may explain why at very low feeds per tooth, the maximum compressive residual stress is measured at the surface. An increase of the feed per tooth leads to a shift of the maximum residual stress to a deeper workpiece region. Results also showed an increase of the compressive residual stresses in the surface and subsurface as the consequence of an increase of the depth of cut in certain range, however the depth of cut does not present any influence on the depth of the layer with the maximum compressive residual stress.
Arrazola et al. [62] developed a finite element model to estimate residual stresses during machining of Nickel based super alloy, where they related residual stresses to material properties like yield stress and friction angle. They have also mentioned the importance of tuning flow stress curves of the material based on the experimental results. The biggest deficiency of finite element models is high computational cost. Lazoglu et al. [63] developed an analytical elasto-plastic model to estimate machining induced residual stresses that overcomes above mentioned deficiency and validated their model via X-ray residual stress measurements on Waspaloy material.
Schulze et al. [64] modeled deflection of the T-profile thin wall made of Aluminum alloy. Authors analyzed an influence of different initial stress states, introduced by 4 point bending operation, and different machining parameters on the amount of distortion via FEM simulations and experimental results. As the result, authors revealed that amount of initial stress has a significant effect on distortion potential. Both simulations and experimental results showed that the increase of the applied force resulted in increased residual stress profiles distortions.
Lazoglu and Mamedov [65] developed a finite element model for simulation of distortions during micro milling process using multi-physics Comsol software. The micro milling process was simulated as a time-dependent multi-physics problem consisting of structural mechanics and heat transfer. The workpiece was loaded with moving heat source and mechanical load at each axial depth of cut for a time period equal to the machining time, as shown in Figure 16. Later, thermal and mechanical loads were removed and distortion was measured as total plastic deformation after elastic recovery of the workpiece. Authors measured the instantaneous deformation of the workpiece during cutting process by laser sensor and permanent distortion of the workpiece after machining by White Light Interferometer, as shown in Figure 17. Instantaneous laser signal contains information on both plastic and elastic deformation. Peaks in the laser signal data correspond to elastic deformation during cutting of the thin wall. The number of peaks equals to a number of cutting passes and FFT frequency analysis of the peak showed that tool passing frequencies are dominant, which means that peaks occur due to the interaction of the tool and workpiece. While, White Light Interferometer measurement results that are coherent with simulation results, shown in Figure 18, correspond to permanent distortion of the workpiece.
Recently, Jia et al. [66] presented a finite element deflection prediction model of micro-milling Inconel 718 thin-walled parts, which reflects the material properties of 718 and the physical properties of the machining process. Initially, finite element simulation model of micro milling Inconel 718 thin walled parts is established. The Johnson-Cook constitutive model is used to describe the constitutive relation and Johnson-Cook failure model at high speed and high strain rate to describe the failure criteria of the thin-walled part material. Later, the predicted value of milling force output from the process simulation model is used as the load in the deformation prediction model. Instead of directly using a model to output the machining deflection, element birth/death technique is used in pursuit of more physical understanding of the deflection mechanics.
 |
Fig. 17 (a) Experimental setup, (b) an illustration of the experimental setup, (c) Microscope view of distorted part, (d) Laser measurement signal of instantaneous deflection of the part during machining [65]. |
 |
Fig. 18 (a) FEM distortion simulation for micro milling at 50 m/min cutting speed, 100 μm axial depth of cut and 10 μm/rev-tooth feed per tooth ratio, (b) Laser distortion measurement, (c) WLI distortion measurement, (d) Comparison of simulation and WLI distortion measurement [65]. |
3 Conclusion and future work
It is important to emphasize that in the last decade the demand for the parts produced with micro machining process has drastically increased. Consequently, micro machining became one of significant industrial manufacturing processes rather than topic of academic research and curiosity. Serious advancements in understanding process nature have been done over last years. This paper presents an overview on different modeling techniques related to modeling of micro milling process and important aspects that authors revealed during their research. Presented work covers aspect of process modeling including chip thickness modeling, force modeling, cutter deflection modeling, thermal and distortion modeling of the micro milling process. Sufficiently accurate modelling of these processes is of great importance because cutting force, cutting temperature, surface roughness etc. can be estimated without numerous experimental work, which is often time and cost consuming. Table 1 summarizes the key scientific studies and their findings in the topic of modelling of the micro-milling process.
Even if, significant process has been made in understanding and modeling of micro cutting process, some complications, unsolved or less understood problems related to final part accuracy and process performance still exist.
Fundamental improvements can be done in order to increase material removal rate, tool life, cost-effectiveness, surface quality and flexibility of the process. Hybrid micro-milling processes, such as ultrasonic vibration-assisted micro-machining, seem to be prospective in achieving these goals by fusing the advantages of the mechanical micro-milling and other advanced technologies. The tool life, surface quality and the process efficiency can be increased by the application of laser supported micromachining technologies.
Due to very tiny cross sections residual stress related distortions are a significant obstacle in front of reduction of the scrap rates during micro milling. One of the future research directions can be the development of a model capable to predict residual stress generation and resulting distortions during milling process. Further, the fundamental understanding of the underlying physics at the origin of generated residual stresses and distortions needs to be introduced and used to perform instantaneous process optimization.
Currently, most of the research related to micro milling deals with relatively simple part geometries, while process modeling for complex geometries requiring multi-axial machining operations has not been thoroughly investigated.
Another aspect to be further developed is machining centers suitable for micro milling. Due to small cutter diameter, to ensure proper cutting speed, spindle speed of the milling centers sometime has to exceed 100.000 rpm. This issue has been partially solved by air spindles, however they struggle from cutting speed control during high load machining operations. Electric motors with magnetic bearing seem to be promising solution as well as bench-type ultra-precision machines will be one of the future development tendencies.
Key scientific studies and their findings.
Acknowledgments
The author would like to thank all researchers and colleagues in field of machining and micro milling for their valuable contributions. Also, would like to apologize for the names that were not included in this limited scope review paper.
References
- J.-D. Kim, D.S. Kim, Theoretical analysis of micro-cutting characteristics in ultra-precision machining, J. Mater. Process. Technol. 49 (1995) 387–398 [CrossRef] [Google Scholar]
- D. Lucca, Y. Seo, R. Komanduri, Effect of tool edge geometry on energy dissipation in ultra-precision machining, CIRP Ann. Manuf. Technol. 42 (1993) 83–86 [Google Scholar]
- K. Liu, X.P. Li, M. Rahman, Characteristics of high speed micro-cutting of tungsten carbide, J. Mater. Process. Technol. 140 (2003) 352–357 [CrossRef] [Google Scholar]
- S.M. Son, H.S. Lim, J.H. Ahn, Effects of the friction coefficient on the minimum cutting thickness in micro cutting, Int. J. Mach. Tools Manuf. 45 (2005) 529–535 [Google Scholar]
- M. Vogler, S. Kapoor, R. DeVor, On the modeling and analysis of machining performance in micro-end milling, part II: cutting force prediction, Trans. ASME J. Manuf. Sci. Eng. 126 (2004) 695–705 [Google Scholar]
- M. Martellotti, An analysis of milling process, ASME J. Manuf. Sci. Eng. 63 (1941) 677–700 [Google Scholar]
- W. Bao, Modeling micro-end-milling operations. Part I: analytical cutting force model, Int. J. Mach. Tools Manuf. 40 (2000) 2155–2173 [Google Scholar]
- W.Y. Bao, I.N. Tansel, Modeling micro end milling operations. Part II: tool run-out, Int. J. Mach. Tools Manuf. 40 (2000) 2175–2192 [Google Scholar]
- H.Z. Li, K. Liu, X.P. Li, A new method for determining the undeformed chip thickness in milling, J. Mater. Process. Technol. 113 (2001) 378–384 [Google Scholar]
- X.P. Li, H.Z. Li, Theoretical modelling of cutting forces in helical end milling with cutter runout, Int. J. Mech. Sci. 46 (2004) 1399–1414 [Google Scholar]
- Y.H. Kang, C.M. Zheng, Mathematical modelling of chip thickness in micro-end- milling: a Fourier modelling, Appl. Math. Model. 37 (2013) 4208–4223 [Google Scholar]
- A. Mamedov, I. Lazoglu, An evaluation of micro milling chip thickness models for the process mechanics, Int. J. Adv. Manuf. Technol. 87 (2016) 1843–1849 [Google Scholar]
- X. Jin, Y. Altintas, Prediction of micro-milling forces with finite element method, J. Mater. Process. Technol. 212 (2012) 542–552 [Google Scholar]
- Y. Altintas, S.S. Park, Dynamic compensation of spindle-integrated force sensors, Ann. CIRP 53 (2004) 305–308 [Google Scholar]
- S.S. Park, M. Malekian, Mechanistic modeling and accurate measurement of micro end milling forces, CIRP Ann. Manuf. Technol. 58 (2009) 49–52 [Google Scholar]
- A. Mamedov, I. Lazoglu, Micro ball-end milling of freeform titanium parts, Adv. Manuf. 3 (2015) 263–268 [Google Scholar]
- M. Malekian, S.S. Park, M.B.G. Jun, Modeling of dynamic micro-milling cutting forces, Int. J. Mach. Tools Manuf. 49 (2009) 586–598 [Google Scholar]
- M.B.G. Jun, X. Liu, R.E. DeVor, S.G. Kapoor, Investigation of the dynamics of microend milling—part I: model development, J. Manuf. Sci. Eng. 128 (2006) 893–900 [Google Scholar]
- N. Fang, Slip-line modeling of machining with a rounded-edge tool—part I: new model and theory, J. Mech. Phys. Solids 51 (2003) 715–742 [CrossRef] [Google Scholar]
- N. Fang, I.S. Jawahir, An analytical predictive model and experimental validation for machining with grooved tools incorporating the effects of strains, strain-rates, and temperatures, CIRP Ann. Manuf. Technol. 51 (2002) 83–86 [Google Scholar]
- X. Jing, H. Li, J. Wang, Y. Tian, Modelling the cutting forces in micro-end-milling using a hybrid approach, Int. J. Adv. Manuf. Technol. 73 (2014) 1647–1656 [Google Scholar]
- Y. Altintas, Manufacturing Automation, Cambridge University Press, 2000 [Google Scholar]
- X. Jing, R. Lv, Y. Chen, Y. Tian, H. Li, Modelling and experimental analysis of the effects of run out, minimum chip thickness and elastic recovery on the cutting force in micro-end-milling, Int. J. Mech. Sci. 176 (2020). https://doi.org/10.1016/j.ijmecsci.2020.105540. [CrossRef] [Google Scholar]
- Y. Zhang, S. Li, K. Zhu, Generic instantaneous force modeling and comprehensive real engagement identification in micro-milling, Int. J. Mech. Sci. 176 (2020). https://doi.org/10.1016/j.ijmecsci.2020.105504. [CrossRef] [Google Scholar]
- A. Mamedov, K.S.E. Layegh, I. Lazoglu, Instantaneous tool deflection model, Int. J. Adv. Manuf. Technol. 79 (2015) 769–777 [Google Scholar]
- Z. Sun, S. Toa, Sh. Zhanga, G. Zhang, Theoretical and experimental unvestigation into non-uniformity of surface generation in micro-milling, Int. J. Mech. Sci. 140 (2018) 313–324 [Google Scholar]
- S.P. Leo Kumar, Experimental investigations and empirical modeling for optimization of surface roughness and machining time parameters in micro end milling using Genetic Algorithm, Measurement 124 (2018) 386–394 [Google Scholar]
- K. Aslantas, E. Ekici, A. Cicek, Optimization of process parameters for micro milling of Ti-6Al-4V alloy using Taguchi-based gray relational analysis, Measurement 128 (2018) 419–427 [Google Scholar]
- G. Beruvides, F. Castaño, R. Quiza, R. Haber, Surface roughness modeling and optimization of tungsten–copper alloys in micro-milling processes, Measurement 86 (2016) 246–252 [Google Scholar]
- K. Vipindas, M. Jose, Wear behavior of TiAlN coated WC tool during micro end milling of Ti-6Al4V and analysis of surface roughness, Wear 424–425 (2019) 165–182 [Google Scholar]
- W. Chen, W. Xie, D. Huo, K. Yang, A novel 3D surface generation model for micro milling based on homogeneous matrix transformation and dynamic regenerative effect, Int. J. Mech. Sci. 144 (2018) 146–157 [Google Scholar]
- Y. Altintas, D. Montgomery, Mechanism of cutting force and surface generation in dynamic milling, J. Eng. Ind. 113 (1991) 160–168 [Google Scholar]
- T. Schmitz, S.K. Smith, Machining Dynamics: Frequency Response to Improved Productivity, Springer Science & Business Media, 2008 [Google Scholar]
- W. Chen, L. Zheng, W. Xie, K. Yang, D. Huo, Modelling and experimental investigation on textured surface generation in vibration-assisted micro-milling, J. Mater. Process. Technol. 266 (2019) 339–350 [Google Scholar]
- X. Zhang, T. Yu, J. Zao, Surface generation modeling of micro milling process with stochastic tool wear, Precis. Eng. 61 (2020) 170–181 [Google Scholar]
- W. Chen, W. Xie, D. Hou, K. Yang, A novel 3D surface generation model for micro milling based on homogeneous matrix transformation and dynamic regenerative effect, Int. J. Mech. Sci. 144 (2018) 146–157 [Google Scholar]
- T. Matsumara, T. Ono, Cutting process of glass with inclined ball end mill, J. Mater. Process. Technol. 200 (2008) 356–363 [Google Scholar]
- T. Matsumara, T. Ono, Influence of tool inclination on brittle fracture in glass cutting with ball end mills, J. Mater. Process. Technol. 202 (2008) 61–69 [Google Scholar]
- X. Liu, R.E. DeVor, S.G. Kapoor, Model-based analysis of the surface generation in microendmilling—part I: model development, J. Manuf. Sci. Eng. 129 (2007) 453–460 [Google Scholar]
- K. Groß, M. Eifler, K. Kauer, K. Huttenlochner, B. Kirsch, C. Zeigler, J.C. Aurich, J. Seewig, Determination of the surface topography of ball end micro milled material measures, Eng. Sci. Technol. (2020) https://doi.org/10.1016/j.jestch.2020.08.005 [Google Scholar]
- R. Komanduri, Z.B. Hou, Thermal modeling of the metal cutting process: part I − temperature rise distribution due to shear plane heat sourse, Int. J. Mech. Sci. 42 (2000) 1715–1752 [Google Scholar]
- R. Komanduri, Z.B. Hou, Thermal modeling of the metal cutting process: part II − temperature rise distribution due to frictional heat sourse at the tool-chip interface, Int. J. Mech. Sci. 43 (2001) 57–88 [Google Scholar]
- R. Komanduri, Z.B. Hou, Thermal modeling of the metal cutting process: part III- temperature rise distribution due to the combined effects of shear plane heat source and the tool chip interface frictional heat source, Int. J. Mech. Sci. 43 (2001) 89–107 [Google Scholar]
- I. Lazoglu, Y. Altintas, Prediction of tool and chip temperature in continuous and interrupted machining, Int. J. Mach. Tools Manuf. 42 (2002) 1011–1022 [Google Scholar]
- I. Lazoglu, C. Islam, Modeling of 3D temperature fields for oblique machining, CIRP Ann. Manuf. Technol. 61 (2012) 127–130 [Google Scholar]
- S. Lin, F. Peng, J. Wen, Y. Liu, R. Yan, An investigation of workpiece temperature variation in end milling considering flank rubbing effect, Int. J. Mach. Tools Manuf. 73 (2013) 71–86 [Google Scholar]
- K. Yang, Y. Liang, K. Zheng, Q. Bai, W. Chen, Tool edge radius effect on cutting temperature in micro-end-milling process, Int. J. Adv. Manuf. Technol. 52 (2010) 905–912 [Google Scholar]
- D.L. Wissmiller, F.E. Pfefferkorn, Micro end mill tool temperature measurement and prediction, J. Manuf. Process. 11 (2009) 45–53 [Google Scholar]
- A. Mamedov, I. Lazoglu, Thermal analysis of micro milling titanium alloy Ti-6Al-4V, J. Mater. Process. Technol. 229 (2016) 659–667 [Google Scholar]
- T. Ozel, T. Thepsonthi, D. Ulutan, B. Kaftanoglu, Experiments and finite element simulations on micro-milling of Ti–6Al–4V alloy with uncoated and CBN coated micro-tools, CIRP Ann. Manuf. Technol. 60 (2011) 85–88 [Google Scholar]
- E.E. Yilmaz, E. Budak, H.N. Ozguven, Modeling and measurement of micro end mill dynamics using inverse stability approach, Proc. CIRP 46 (2016) 242–245 [Google Scholar]
- S.S. Park, R. Rahnama, Robust chatter stability in micro-milling operations, CIRP Ann. Manuf. Technol. 59 (2010) 391–394 [Google Scholar]
- R. Rahnama, M. Sajjadi, S.S. Park, Chatter suppression in micro end milling with process damping, J. Mater. Process. Technol. 209 (2009) 5766–5776 [Google Scholar]
- E. Graham, M. Mehrpouya, R. Nagamune, S.S. Park, Robust prediction of chatter stability in micro milling comparing edge theorem and LMI, CIRP J. Manuf. Sci. Technol. 7 (2014) 29–39 [Google Scholar]
- K.K. Singh, V.K.R. Singh, Component mode synthesis approach for micro end mill dynamics considering machine tool compliance, Proc. CIRP 58 (2017) 469–474 [Google Scholar]
- A. Mokhtari, M.M. Jalili, A. Mazidi, M.M. Abootorabi, Size dependent vibration analysis of micro-milling operations with process damping and structural nonlinearities, Eur. J. Mech. A Solids 76 (2019) 57–69 [Google Scholar]
- I.S. Jawahir, E. Brinksmeier, R. M'Saoubi, D.K. Aspinwall, J.C. Outeiro, D. Meyer, D. Umbrello, A.D. Jayal, Surface integrity in material removal processes: recent advances, CIRP Ann. Manuf. Technol. 60 (2011) 603–626 [Google Scholar]
- C.O. Ruud, A review of selected non-destructive methods for residual stress measurement, NDT Int. 15 (1982) 15–23 [Google Scholar]
- H.K. Tönshoff, T. Friemuth, J.C. Becker, Process monitoring in grinding, Ann. CIRP 51 (2002) 551–571 [Google Scholar]
- E. Brinksmeier, State of the art non destructive measurement of subsurface material properties and damages, Prec. Eng. 11 (2002) 211–224 [Google Scholar]
- B. Denkena, D. Boehnke, L. León, Machining induced residual stress in structural aluminum parts, Prod. Eng. 2 (2008) 247–253 [Google Scholar]
- P. Arrazola, A. Kortabarria, A. Madariaga, J. Esnaola, E. Fernandez, C. Cappellini, D. Ulutan, T. Özel, On the machining induced residual stresses in IN718 nickel-based alloy: experiments and predictions with finite element simulation, Simul. Model. Pract. Theory 41 (2014) 87–103 [Google Scholar]
- I. Lazoglu, D. Ulutan, B.E. Alaca, S. Engin, B. Kaftanoglu, An enhanced analytical model for residual stress prediction in machining, CIRP Ann. Manuf. Technol. 57 (2008) 81–94 [Google Scholar]
- V. Schulze, P. Arrazola, F. Zanger, J. Osterried, Simulation of distortion due to machining of thin-walled components, Proc. CIRP 8 (2013) 45–50 [Google Scholar]
- I. Lazoglu, A. Mamedov, Deformation of thin parts in micro milling, CIRP Ann. Manuf. Technol. 65 (2016) 117–120 [Google Scholar]
- Z. Jia, X. Lu, H. Gu, F. Ruan, S.Y. Liang, Deflection prediction of micro-milling Inconel 718 thin-walled parts, J. Mater. Process. Technol. 291 (2021). https://doi.org/10.1016/j.jmatprotec.2020.117003. [Google Scholar]
Cite this article as: Ali Mamedov, Micro milling process modeling: a review, Manufacturing Rev. 8, 3 (2021)
All Tables
All Figures
 |
Fig. 1 Comparison of cutting forces and the frequency spectrums at: n = 10 000 rpm, c = 3 µm/tooth, a = 50 µm [13]. |
| In the text | |
 |
Fig. 2 The division of slip-line field. (a) Three major shear zones. (b) A total of 27 slip-line sub regions [19]. |
| In the text | |
 |
Fig. 3 Simulated and experimental deflection values of the tool tip in x and y direction for depth of cut 100 μm and feedrate 5 μm/rev-tooth under down-milling cutting condition [25]. |
| In the text | |
 |
Fig. 4 A model proposed to predict relative standard deviation of surface roughness [26]. |
| In the text | |
 |
Fig. 5 Finished surface characteristic and cross-sectional 2D profile with depth of cut at 10 µm and feed rate 0.8 µm/flute [26]. |
| In the text | |
 |
Fig. 6 Surface roughness variation with tool wear with (a) 5 μm/tooth feed rate, (b) 0.3 μm/tooth feed rate [30]. |
| In the text | |
 |
Fig. 7 Stability lobes diagram [31]. |
| In the text | |
 |
Fig. 8 Simulated surface at spindle speed of 80 000 rpm. (a) without considering the machining dynamics; (b) considering the machining dynamics; (c) experimental result [31]. |
| In the text | |
 |
Fig. 9 Flow chart of the surface simulation process [34]. |
| In the text | |
 |
Fig. 10 Predicted and measured surface topography of micro milling process with spindle speed 20 000 rpm, feed rate 0.2 mm/ s, radial depth of cut 0.508 mm, and axial depth of cut 0.15 mm [35]. |
| In the text | |
 |
Fig. 11 Schematic of the heat transfer model with a common coordinate system for the combined effect of two principal heat sources: the shear plane heat source and the tool-chip interface frictional heat source [43]. |
| In the text | |
 |
Fig. 12 Heat transfer model and heat partition into workpiece [46]. |
| In the text | |
 |
Fig. 13 Heat source application zones [49]. |
| In the text | |
 |
Fig. 14 Comparison of robust stability lobes with analytical stability lobes and experimental chatter points [54]. |
| In the text | |
 |
Fig. 15 (a) Idealized micro end mill; (b) Micro end mill with machine tool compliance [55]. |
| In the text | |
 |
Fig. 16 (a) CAM model of the workpiece; (b) FE model of the distortion simulation [65]. |
| In the text | |
 |
Fig. 17 (a) Experimental setup, (b) an illustration of the experimental setup, (c) Microscope view of distorted part, (d) Laser measurement signal of instantaneous deflection of the part during machining [65]. |
| In the text | |
 |
Fig. 18 (a) FEM distortion simulation for micro milling at 50 m/min cutting speed, 100 μm axial depth of cut and 10 μm/rev-tooth feed per tooth ratio, (b) Laser distortion measurement, (c) WLI distortion measurement, (d) Comparison of simulation and WLI distortion measurement [65]. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


