EDP Sciences logo
Submit your paper
Search
Menu
Home All issues Volume 9 (2022) Manufacturing Rev., 9 (2022) 18 Full HTML
Open Access
Issue
Manufacturing Rev.
Volume 9, 2022
Article Number 18
Number of page(s) 12
DOI https://doi.org/10.1051/mfreview/2022017
Published online 04 July 2022

© A. Vergnano et al., Published by EDP Sciences 2022

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

Permanent die design for Al alloy casting must meet the increasing demand for robust quality. Production efficiency and cost reduction have to be pursued in order to remain competitive in a rapidly changing and challenging market. Usually, each permanent die is manufactured as a one-off prototype, or in very few-offs, but it will have to deliver between 80,000 and 100,000 quality castings during its service life. Therefore, it must be very reliable and fully operational from first use. Design choices for a permanent die are critical [1], since they require in-depth knowledge of fluid flow, heat transfer and solidification dynamics [2], together with material physics [3].

The reduction of scrap, i.e. defective castings, is one of the first objectives for both quality improvement and cost reduction. In die casting, most scrap is due to porosity defects, which are voids or holes in the material that significantly reduce the casting strength [4] and fatigue behavior [5,6]. However, such defects should be avoided even before starting the actual die manufacturing. For that purpose, research works study methods for predicting the probability of occurrence of porosity defects [7–12]. However, this requires very accurate models of both the process [13,14] and the micro-physics [15,16] of each specific alloy, usually backed by Design of Experiments techniques [17,18] in order to identify the vital parameters in the process [19] together with their optimal robust values [20,21]. In this framework, the occurrence of porosities can be reduced with proper design choices that guarantee progressive solidification dynamics [22–24]. Many research works have investigated the positioning [25], shaping [26] and sizing of feeders [27]. Due to its great thermal inertia, a feeder is the last to be solidified, hence it attracts the solidification dynamics towards its location [28], feeding the casting shrinkage for longer [29]. On the other hand, the feeder size must be kept low since this is waste material that must be removed from the casting after cooling.

The grain size of the Al alloy has to be as small as possible in order to obtain good mechanical properties, as the yield strength [30] and the ultimate tensile strength [31,32] are inversely proportional to the square root of the grain size. Thus, for production quality control, the expected Al alloy strength is indirectly verified by measuring the grain size as Secondary Dendrite Arm Spacing (SDAS) on micrographs of polished and etched samples [33]. The SDAS values in critical zones are so important, also affecting the occurrence of defects, that they are usually set as contract specifications with the foundry. Literature demonstrates that the SDAS can be reduced by reducing the solidification time [34–36].

In order to achieve porosity, production cycle time and SDAS specifications, heat removal from the molten and solidifying alloy is a key factor to be generally enhanced [37–39]. Besides die cooling with air or water flowing into channels [40], the heat removal rates are also influenced by the insulating coatings on the die surfaces [41–43] or even by air gaps [44] which locally increase the thermal resistance. On the other hand, heat flow enhancement cannot be pursued by reducing the coating thickness, since this would lead to premature die wear. Finally, the overall heat removal performances are also limited by the heat transfer resistance of the steel die insert. In fact, these must be very thick in order to guarantee the expected die life.

This work aims to investigate the possibility to decrease the overall casting cost, by improving the process yield while reducing the cycle time. In particular, the die is considered as a complex thermal machine, with the main function of removing heat from the casting, waiting for it to be frozen into the designed shape. The research question is if the increased heat removal rate of the die due to a steel with enhanced thermal conductivity, despite its higher investment cost, leads to savings in the overall unit cost of the castings. In particular, the possibility to design the die inserts with 1.2383 steel is investigated here. In fact, 1.2383 steel has enhanced thermal conductivity compared to the more common 1.2343 [45,46]. Nowadays, computer simulations with complex models are reliable design tools for handling complex and multi-physics phenomena [47–49]. Therefore, simulation experiments are run with a sequence of designs considering combinations of inserts made of different steels.

The paper is organised as follows: Section 2 introduces the method for the design and evaluation of simulation experiments, Section 3 presents a case study on an engine head produced in GDC and discusses the results, while Section 4 draws the concluding remarks.

2 Method for yield and cycle time improvements in Al alloy die casting

A die is a complex thermal machine, and its design process involves the definition of many parameters. The fluid flow, heat transfer and solidification dynamics in the process must be carefully engineered in order to achieve the demanded metallurgical properties in the final parts. Moreover, starting with an already effectively engineered die, two design parameters, namely the selection of the die material and its cooling operation, can be investigated in order to search for further cycle time and yield improvements.

In this study, as shown in Figure 1, different die designs are defined, with a full factorial combination of different layouts of steel cavity inserts and cooling channel operating fluids. The feeders are sized by simulation to achieve the expected quality levels. Thereafter, the candidate design solutions are compared in terms of casting yield, cycle time and SDAS. The investment and variable costs are then evaluated in order to calculate the overall casting cost for the specific design. Final decisions are taken after the evaluation by foundry engineers and customer management.

thumbnail Fig. 1

Method for yield and cycle time improvements through the evaluation of die designs with different layouts of steel cavity inserts and cooling channels.

2.1 Casting cost evaluation

In this method, the cost is the objective function to be minimized, as in Sarma and Adeli [50] and in Favi et al. [51] and. The casting unit cost [€], is determined as 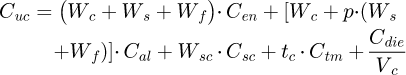(1)

where the weight [kg] of the casting, Wc, the casting system, Ws, and the feeders, Wf, are considered and Cen [€/kg] is the energy unit cost for melting them in each cycle. The material in Ws and Wf will be cut away, re-melted and reconditioned to be reused in next production. Nevertheless, a certain amount of waste must be considered in this recycling process. So, p [−] is a waste coefficient in the Ws + Wf recycling, p = 0.15 from foundry experience. Cal [€/kg] is the alloy material unit cost. Wsc [kg] is the weight of all sand cores, while Csc [€/kg] is the unit cost of cores. tc [s] is the cycle time and Ctm [€/s] considers the maintenance, labour and general running cost of the die. Finally, Cdie [€] is the investment cost of the die equipment and Vc is the total production volume in the expected die lifetime.

The energy unit cost is (2)

where Ceu [€/kJ] is the cost of the energy used in the foundry and Qal [kJ/kg] is the heat necessary for melting and heating up to the pouring temperature 1 kg of alloy. Qal is (3)

where ΔTal [° C] is the temperature increase from room temperature, 20 ° C, to the pouring temperature, cp [kJ/(kgK)] is the specific heat capacity, averaged through the ΔTal range, and Lal [kJ/kg] is the latent heat of the alloy.

The cost of the die equipment can be estimated as (4)

where nins [−] is the number of inserts of the die, Wins,i [kg] is the weight of the ith insert, Cst,i [€/kg] and Cmfg,i [€/kg] are respectively the unit costs for the steel material used in the insert and for its manufacturing.

The construction of the insert in 1.2383 steel, rather than 1.2343, is expected to improve the heat removal rate. Therefore, the variable Wf and the result tc are expected to reduce and the first, second and fourth terms of (1) accordingly. Conversely, the fifth term increases due to the higher costs of the 1.2383 steel. The fourth term is constant, since no modifications to the cores are possible using this method.

2.2 Steel selection for die inserts

The steel of the cavity inserts, in contact with the solidifying casting, must have good properties of resistance to soldering, erosion and thermal fatigue cracking. This is because a molten Al alloy, poured at a temperature of 680–740 °C, is very aggressive due to its high chemical activity [52,53]. Few steels can be selected for manufacturing a die for GDC. The soft annealed C40 and the quenched and tempered 1.2311 are suitable only for small production series or for dies operating under low thermomechanical loads. These two are selected when their low cost for purchase and for heat treatment is very valued. On the other hand, their hardness is very low, as about 220 HB for the C40 [54] and 280–325 HB for the 1.2311 [55]. This makes them prone to fast surface wearing. Due to these limitations, the most commonly used steel for the construction of die inserts is 1.2343, also called X38CrMoV5-1 in the DIN standard, because of its good combination of properties of yield strength and resistance to hot cracking [56,57]. Since the 1.2343 has a higher application hardness level after quenching and tempering, about 352–390 HB [58], it shows higher yield and ultimate strength in hot conditions. Also, since 1.2343 steel is alloyed with Cr, Mo and V, it shows a better resistance to thermal fatigue than C40 and 1.2311.

The layout of the die cavity inserts of different steels is the first design variable of this method. 1.2343 steel is compared with 1.2383 [59], also called Thermodur® 2383 Supercool. The latter preserves the high properties offered by 1.2343, but it is renowned for its enhanced thermal conductivity, high heat checking resistance and very good tempering resistance. Figure 2 shows the thermal conductivity of 1.2383 steel compared with 1.2343. In the current temperature operating range for die steel during Al casting, from about 200 °C to 400 °C, the thermal conductivity increases by 40%–50%. This significant increase suggests that the use of 1.2383 would improve the heat removal rate and generally reduce the casting solidification time, thus anticipating casting ejection and reducing the cycle time. As for the chemical composition, the most important difference is the total absence of Cr in 1.2383 [60]. The tempering behavior is slightly different, since 1.2383 shows a tempering resistance even 50°C higher than 1.2343. However, comparable results can be obtained by properly tuning the treatment temperatures. The erosion phenomenon is related to the surface hardness and, since 1.2383 and 1.2343 can be used under the same conditions, it is expected that their resistance is comparable. Yield and ultimate strength at high temperatures are also comparable. Regarding thermal fatigue resistance, 1.2383 can show more cracks than 1.2343 during its operation life. However, these are exceptionally short and ultimately the resistance of 1.2383 is considered better. Thanks to its better thermal conductivity, the 1.2383 is able to better dissipate heat from the skin. Therefore, also its soldering resistance is expected to increase.

Three levels are considered here for the layout of steel inserts:

  • All die cavity inserts manufactured in 1.2343 steel;

  • Intermediate solution, with 1.2383 steel selected only for the inserts that must deliver low SDAS, while the others are still manufactured in 1.2343:

  • All die cavity inserts manufactured in 1.2383 steel.

thumbnail Fig. 2

Thermal conductivity of 1.2343 and 1.2383 steels [59,60].

2.3 Cycle definition and die cooling

A die casting cycle includes the phases of preparation, pouring, solidification and ejection, as shown in Figure 3. The casting cooling after ejection runs in parallel with the subsequent cycles, and is not considered in the cycle time as it is not time-consuming for the foundry production.

After some warm-up cycles, a die must deliver a non-uniform temperature field necessary for solidification without defects and for the production of small material SDAS in the critical zones [61]. The die differential cooling is carried out with cooling channel design solutions [62,63]. The operating fluid for the cooling channels may be water or air, suitably setting the flow rates and on-off times in the cycle [64]. Water cooling channels certainly provide much higher heat removal rates, ensuring faster solidification [65]. On the other hand, they generally make the die operation and safety more complex. In fact, they require additional devices in the die layout, frequent channel cleaning and in some cases sudden boiling may occur, and there may even be a risk of explosion if the die cracks. Conversely, air cooling is less performing, but has a much safer operation. The cooling channel operation is the second design variable of this method. It is considered with two levels:

  • a: air operated;

  • w: water operated.

The channel path, flow rates and on-off times in the cycle are non-variable. For notation purposes, the combination of the 1-, 2-, 3- and the −a, −w variable levels delivers six design cases, referred to as 1a, 1w, 2a, 2w, 3a, 3w. For the final evaluations, the original design is assumed as the benchmark solution. Quite often this is the 1w case.

thumbnail Fig. 3

Typical process phases in a die casting cycle.

2.4 Feeder design

The feeders are responsible for feeding the casting solidification and the consequent volume shrinkage. From a practitioner point of view, it is usually good for quality improvement, i.e., to reduce porosities, increase the neck [66] and the size [67] of the feeders. On the other hand, the reduced cost thanks to scrap reduction may be jeopardized by longer solidification times and by larger molten metal volume to be fed for each casting. In addition, if the necks are too large, they could cause technological problems in the feeders cutting phase.

In this method, the neck of each feeder is designed as large as possible, depending on the aforementioned technological limitations. Hence, the feeders are sized recurring to simulations. The first modelled configuration is the minimum size in the search range. Thereafter, this is progressively increased in order to achieve the expected quality in terms of porosity defects.

2.5 Porosity defect evaluation

Several sources of porosity can be described [68,69]. Firstly, gas porosity consists in the formation of bubbles in the casting [70]. This occurs because a liquid alloy can host a large amount of dissolved gas, the solubility of which progressively decreases as solidification progresses. Therefore, the gas forms bubbles in the material as it cools. This porosity can be controlled by the careful design of the alloy composition, the geometry of die cavities and the pouring parameters.

Another dangerous source of porosity is shrinkage [12,16,19]. In particular, during solidification, an Al alloy experiences a drop of the specific volume, from about 0.42*10-3 m3/kg to 0.37*10-3 m3/kg, so more than −10%. This shrinkage has to be compensated by being fed by the surrounding still-liquid alloy. Shrinkage porosity arises when the liquid volume of a casting solidifies later than the surrounding volumes, so it is no longer connected to a liquid feeder. The subsequent solidification and shrinkage of this volume cannot be compensated by a liquid flow and therefore a vacuum is generated.

In this method, porosity is the first performance output and is evaluated with a casting simulation. A specified probability of porosity occurrence is an objective function for feeders sizing. It should be noted that a small probability of occurrence is unavoidable in die casting, and has to be defined resorting to experience. The six design cases with properly sized feeders are then submitted for the subsequent evaluation of the technical performances.

2.6 Casting yield

The size of the feeders has a direct consequence on the casting yield, defined as the weight ratio of the casting by the total amount of alloy to be poured in the cycle [71] (5)

Although secondary to quality, the casting yield must be maximised, as this reduces the material waste, the energy used to melt the alloy as well as the heat to be removed by the die [72–74]. The casting yield is the second output evaluated by simulation, because its improvement would lead to a direct reduction of costs.

2.7 Cycle time

This method assumes that the fluid dynamics in the die casting system and all the other equipment in the foundry are already effectively engineered. Therefore, the preparation, pouring and ejection phases, referring to Figure 3, are not considered for modification. Therefore, the only phase affecting the cycle time is solidification. In fact, the casting can be ejected only after complete solidification, thus when the alloy is cooled at least to its Solidus temperature [75]. Therefore, the die open condition is parameterised in the simulations only as waiting for the casting to completely solidify. Hence, the die open time is the third evaluated variable in the casting cycle.

2.8 Secondary dendrite arm spacing evaluation

The fourth output evaluated is the SDAS in the zones defined as critical by the casting part designer. The SDAS, measured in [μm], is important in this method as it is strongly influenced by the heat removal rate. From literature (6)

where ts is the solidification time [s], k and n are characteristic constants [–] for the alloy. As a rule of thumb, the SDAS is approximately proportional to the cube root of the solidification time, i.e. the value of n ≈ 0.33, [33,36]. A higher heat removal rate would reduce the solidification time, thus reducing the SDAS and consequently improving the Al alloy strength.

3 Case study on gravity die casting

The method for yield and cycle time improvements, thanks to the construction of the die inserts with an enhanced conductivity steel, is applied here in a case study on GDC. A die for a four-cylinder engine head with bottom pouring layout is studied.

3.1 Original die design

The assembly of the casting, the top feeder, all the cores and the casting system, including the pouring basin, sprue, filter, runner and gates, is shown in Figure 4a. Figure 4b shows the die inserts with different colours, while the blue die structure will not be modified with the method. The geometry of the engine head, the casting process and all the shapes of the die were previously engineered: an AlSi7Mg0.3 alloy was chosen, poured at 740 °C; the spiral-shaped pouring basin leads the initial pouring while reducing turbulence; the progressive narrowing of the sections avoids flow separation and turbulence and limits the velocity at the four gates to 0.5 m/s in order to reduce gas entrapment and die or cores erosion; the filter cleans the alloy from impurity particles and reduces the flow velocity; the core prints enable their assembly and counterbalance the metallostatic thrust; the base insert and the chamber inserts are provided with separated cooling channels inside; the chamber inserts are cooled with a higher flow rate than the base one; the chamber inserts are machined with a 0.1 mm assembly gap with respect to the base insert which produces an additional heat transfer resistance [44], so that the heat removal, focused in the combustion chambers, effectively reduces the SDAS there; the top feeder has an original height of 95 mm, optimised to avoid porosities in the original design. The die inserts are further detailed in the drawings of Figure 4c and in Table 1.

thumbnail Fig. 4

CAD models of (a) the casting cavities and cores, of (b) the complete die and of (c) its inserts in an opened view.
Table 1

CAD overall dimensions and mass properties.

3.2 Simulation of the design cases

The simulations were carried out using Magmasoft [76] with the geometry models of Figure 4 and the process cycle of Figure 3. The mesh size includes 1,390,596 cavity cells, 9,861,826 being the total size. The process phases are modeled as:

  • Die preparation for 35 s: cleaning for 20 s and then core positioning, die closing after further 10 s, 5 s waiting time;

  • Pouring phase: automatic filling control with 70% filled basin, 50 mm inlet height from basin, AlSi7Mg0.3 alloy poured at 740 °C temperature;

  • Solidification until die open: until the maximum temperature inside the alloy falls below the Solidus temperature of 542 °C, considering metal walls are much cooler and stronger so that the casting can be ejected;

  • Casting ejection: a robot approaches, grabs and moves the casting for 15 s;

  • Water cooling: on from 0 to 300 s in the cycle in the water cooled design cases;

  • Air cooling: always on in the air cooled design cases;

  • Casting cooling after ejection: until the maximum temperature inside the alloy falls below 100 °C temperature;

  • Cores: silica sand at 40 °C initial and uniform temperature;

  • Die inserts in 1.2343 or 1.2383 steel, depending on the design case, with 250 °C initial and uniform temperature;

  • Simulation sequence: with 6 heating cycles for the die warm up to the non-uniform temperature field, while the results are evaluated in the 7th cycle.

A summary of the materials configuration for the die inserts in the different design cases is reported in Table 2. In the 1- design cases, all die inserts are made of 1.2343 steel. With reference to Figure 4c, the 2- cases have the base and the combustion chamber inserts made of 1.2383, while the others are still made of the cheaper 1.2343. The 3- cases have all the nine cavity inserts made of 1.2383.

Table 2

Materials selection for the die inserts in the design cases.

3.3 Evaluation of the design cases

The feeder is shown in orange inside the green top core in Figure 4a. Its variable height starts from 70 mm for each design case and is then increased in 5 mm steps. For each simulation, the porosity and solidification results are investigated. Porosity is calculated in the simulations as occurrence probability. Figures 5a and 5b shows the porosity result for case 3a before and after the feeder sizing. The porosity result is shown only for the values above 5% occurrence probability and in a 5–10% scale. Based on calibration in the foundry, <5% means negligible occurrence, 5–10% progressively increases to eventual up to frequent, while >10% means inevitable occurrence.

The solidification results are used to thoroughly analyse the possible porosity formation. As shown in Figure 6, the solidification begins peripherally from the zones in contact with the side walls and mostly from the inserts cooled from below. The results consider only the alloy fraction liquid from 70% to 100%, because, in the simulation model, above 30% fraction solid the AlSi7Mg0.3 alloy is no longer able to flow and feed the neighbouring zones.

The casting yield is calculated with (5) from CAD volumes. The process cycle time is considered from the simulation of each sized design case, resulting from the die open condition after complete alloy solidification. The SDAS is calculated with (6) with the coefficients k = 1.852 and n = 0.5735, since these were previously identified for the same material [33]. For example, Figure 7 reports the solidification times and the SDAS in the critical zones for case 3a. Finally, the costs are calculated with equations (1)–(4).

thumbnail Fig. 5

Porosity occurrence result as simulated for the design case 3a before and after feeder optimization.
thumbnail Fig. 6

Solidification in the 3a optimized case at different (a), (b) and (c) time steps.
thumbnail Fig. 7

Simulation results for (a) the solidification time and (b) the SDAS in the combustion chambers of the engine head for case 3a.

3.4 Results and discussions

The results for the technical evaluation of the six design cases are reported in Table 3.

Considering 1w as the benchmark solution, the casting yield decreases by 0.016 for the simplest 1a design case, while it increases by 0.016 for case 2a and by 0.032 for cases 2w, 3a and 3w thanks to the reduction of the feeder size. Considering 1.2383 steel in place of 1.2343 for the bottom inserts would increase the yield. Redesigning the side insert brings no further improvements, at least considering the 5 mm step for the feeder growth.

From 1a, the cycle time is reduced by 40 s for 2a, and doubled to 88 s for 3a. Similarly, considering 1w, the cycle time is reduced by 51 s for 2w and by 92 s for 3w. On average, compared to the 1- cases, the 2- cases have a 46 s cycle time reduction while the 3- cases a 90 s reduction. The cycle time for the − w cases is reduced by 50 s compared to the − a cases. Compared to the 1w benchmark solution, the most performing 3w show a 92 s cycle time reduction. The cycle time, governed by the heat removal rate, can be significantly reduced through the use of enhanced conductivity steel and/or water cooling solutions. However, the enhanced conductivity of the insert steel appears to be the most important parameter. The reduction of the feeder size thanks to the 1.2383 steel inserts reduces the heat to be removed by the die, with a leverage effect on cycle time.

Case 3w gives the smallest SDAS thanks to faster solidification times. Cases 2w and 3w show slightly improved SDAS compared to 1w. On the other hand, the − w cases show a reduction of 5.7 μm compared to the − a cases. Therefore, the cooling operation is the most important design parameter for achieving quality SDAS. Most likely, efficient die cooling is able to decrease the temperature of the insert surfaces, which causes fast alloy freezing of the casting skin.

A possible limitation of the simulations just discussed can be identified in the model of the heat transfer between casting and die. In fact, this model must take into account the already discussed drop of specific volume during the solidification, which causes the separation between the surfaces of the casting and the die. This is generally valid and modeled globally with a drop in the heat transfer coefficient as a function of temperature [61]. However, it can be expected that this effect will not occur on every surface. In particular, this phenomenon is variable from point to point for the inserts facing in the direction of the force of gravity, such as the base and chamber inserts in this simulation. In this case it can be expected that the coefficient should remain higher nearby the contact points even after the casting solidification. However, this can only be identified by genetic algorithms after the die is already manufactured and working [41,42]. It is difficult to be evaluated in the design phase in a method based on simulations. In the end, it can be expected that the heat removal from the bottom is even more efficient and the improvement of the base and chamber inserts might lead to even greater results.

The estimated casting unit cost is reported in Table 4 for all the terms in (1). The results are reported as the percentage difference from the benchmark design case 1w. In the last column, the total unit cost for the castings, including investment and variable costs, is reported for each design case. The simplest 1a case uses the same die equipment as 1w, but involves an increase in all variable costs. In all the insert layouts, the −a cooling has higher production costs than −w, due to the longer cycle times. The 2- and most of the 3-layouts result in reductions in both energy and material costs. 2a shows a slight production cost increase while 2w, 3a and 3w show significant reductions. The die cost is clearly higher for 2- and most of the 3- layouts. No costs savings are considered here for the −a cooling compared to that of the −w, since the dies are mounted on machines equipped with all the necessary equipment for both. The die cost is spread over 100,000 castings. The total costs for each casting increases for the 1a design cases but progressively decreases for the 2a, 3a and 2w, up to −5.3% for 3w.

The production capacity of the six design cases is reported in Table 5. In comparison with the 1w case, the estimated ROI is reported in terms of pieces to be produced or in work shifts. For the most performing 3w case, the cost increase is returned in just 34 shifts.

Table 3

Input variables, simulation and evaluation outputs for the six design cases.

Table 4

Cost estimation of the six design cases with respect to 1w design case.

Table 5

Production capacity of the six design cases.

4 Conclusions

This research presents a method for the improvement in yield and productivity of a die design. The evaluation by simulation of design cases with different combinations of 1.2343 or 1.2383 steel inserts and water- or air-cooled channels is explained. In the operating temperature range for an Al alloy gravity casting die, thermal conductivity of 1.2383 steel is about 40–50% higher than 1.2343. Therefore, the inserts made of 1.2383 steel have a higher heat removal rate. Of course, for cooling, water performs better than air. Other than the original input design with all inserts in 1.2343, two new layouts are investigated, the first being an intermediate solution with the replacement of the most important inserts, and the second the complete solution with the full set replacement. The sizing of the feeders for delivering the expected quality levels already leads to significant yield improvements.

A case study on a GDC die for an actual AlSi7Mg0.3 engine head is presented. The layouts with 1.2383 inserts and water cooling allow the feeder size to be reduced. The combined effects of a higher heat removal rate and reduced heat to be removed result in significant cycle time savings.

The die inserts made of 1.2383 steel require greater investments in die equipment, but the improved performance leads to quicker ROI. Considering the layout with all the die cavity inserts manufactured with 1.2383 steel, the designers and the management can choose whether to use the safer and simpler air cooling, with a 3.0% cost reduction and a 64-shift ROI, or the better performing water cooling, with a 5.3% cost reduction and 34-shift ROI.

The method introduced in this research leads to significant improvement in performance and costs for a foundry. Future works will investigate if steel with enhanced thermal conductivity could also improve the die service life, by reducing the thermal fatigue that causes cracks on the surface of inserts, corrosion and soldering of Al alloy.

References

  1. C. Panseri, Manuale di Fonderia D’alluminio, U. Hoepli, Milan, IT (1966) pp. 550–609, in Italian [Google Scholar]
  2. J. Campbell, Castings, Elsevier Butterworth-Heinemann, Oxford, UK (2003) pp. 70–177 [CrossRef] [Google Scholar]
  3. J.T. Black, R.A. Kohser, DeGarmo’s materials and processes in manufacturing (John Wiley & Sons, 2021), pp. 106–124 [Google Scholar]
  4. G.W. Mugica, D.O. Tovio, J.C. Cuyas, A.C. González, Effect of porosity on the tensile properties of low ductility aluminum alloys, Mater. Res. 7 (2004) 221–229 [CrossRef] [Google Scholar]
  5. J. M. Boileau, J. E. Allison, The effect of porosity size on the fatigue properties in a cast 319 aluminum alloy, SAE Transact. 110 (2001) 648–659 [Google Scholar]
  6. H.R. Ammar, A.M. Samuel, F.H. Samuel, Porosity and the fatigue behavior of hypoeutectic and hypereutectic aluminum-silicon casting alloys, Int. J. Fatigue 30 (2008) 1024–1035 [CrossRef] [Google Scholar]
  7. E.J. Whittenberger, F.N. Rhines, Origin of porosity in castings of magnesium-aluminum and other alloys, JOM 4 (1952) 409–420 [CrossRef] [Google Scholar]
  8. H.S. Whitesell, R.A. Overfelt, Influence of solidification variables on the microstructure, macrosegregation, and porosity of directionally solidified Mar-M247, Mater. Sci. Eng. A 318 (2001) 264–276 [CrossRef] [Google Scholar]
  9. Z. Lei, L. Hengcheng, P. Ye, W. Qigui, S. Guoxiong, In-situ observation of porosity formation during directional solidification of Al-Si Casting Alloys, Res. Dev. (2011) https://en.cnki.com.cn/Article_en/CJFDTotal-ZZ AF201101005. htm [Google Scholar]
  10. D. Concer, P.V.P. Marcondes, Experimental and numerical simulation study of porosity on high-pressure aluminum die casting process, J. Braz. Soc. Mech. Sci. 39 (2017) 3079–3088 [CrossRef] [Google Scholar]
  11. S. Mozammil, J. Karloopia, P.K. Jha, Investigation of porosity in Al casting, Mater. Today: Proc. 5 (2018) 17270–17276 [CrossRef] [Google Scholar]
  12. V. Khalajzadeh, D.D. Goettsch, C. Beckermann, Real-time X-ray radiography and computational modeling of shrinkage porosity formation in aluminum alloy castings, Metall. Mater. Trans. A 50 (2019) 757–771 [CrossRef] [Google Scholar]
  13. K. Kubo, R.D. Pehlke, Mathematical modeling of porosity formation in solidification, Metall. Trans. B 16 (1985) 359–366 [CrossRef] [Google Scholar]
  14. D. Sui, Z. Cui, R. Wang, S. Hao, Q. Han, Effect of cooling process on porosity in the aluminum alloy automotive wheel during low-pressure die casting, Int. J. Metalcast. 10 (2016) 32–42 [CrossRef] [Google Scholar]
  15. A.S. Sabau, S. Viswanathan, Microporosity prediction in aluminum alloy castings, Metall. Mater. Trans. B 33 (2002) 243–255 [CrossRef] [Google Scholar]
  16. J. Jakumeit, S. Jana, B. Böttger, R. Laqua, M.Y. Jouani, A. Bührig-Polaczek, Simulation-based prediction of micro-shrinkage porosity in aluminum casting: fully-coupled numerical calculation vs. criteria functions, IOP Conf. Ser. Mater. Sci. 27 (2012) 012066 [Google Scholar]
  17. G.O. Verran, R.P.K. Mendes, L.V.O. Dalla Valentina, DOE applied to optimization of aluminum alloy die castings, J. Mater. Process. Tech. 200 (2008) 120–125 [CrossRef] [Google Scholar]
  18. U.A. Dabade, R.C. Bhedasgaonkar, Casting defect analysis using design of experiments (DoE) and computer aided casting simulation technique, Proc. Cirp 7 (2013) 616–621 [CrossRef] [Google Scholar]
  19. D.R. Gunasegaram, D.J. Farnsworth, T.T. Nguyen, Identification of critical factors affecting shrinkage porosity in permanent mold casting using numerical simulations based on design of experiments, J. Mater. Process. Tech. 209 (2009) 1209–1219 [CrossRef] [Google Scholar]
  20. V.D. Tsoukalas, Optimization of porosity formation in AlSi9Cu3 pressure die castings using genetic algorithm analysis, Mater. Des. 29 (2008) 2027–2033 [CrossRef] [Google Scholar]
  21. V.S. Gondkar, K.H. Inamdar, Optimization of casting process parameters through simulation, Int. J. Appl. Innov. Eng. Manag. 3 (2014) 276–283 [Google Scholar]
  22. F. Chiesat, R. Fuoco, J.E. Gruzleski, Porosity distribution in directionally solidified test bars sand cast from a controlled A356 melt, Cast Met. 7 (1994) 113–122 [CrossRef] [Google Scholar]
  23. Z. Sun, H. Hu, X. Chen, Numerical optimization of gating system parameters for a magnesium alloy casting with multiple performance characteristics, J. Mater. Process. Technol. 199 (2008) 256–264 [CrossRef] [Google Scholar]
  24. Z. Gao, W. Jie, Y. Liu, H. Luo, Solidification modelling for coupling prediction of porosity and segregation, Acta Mater. 127 (2017) 277–286 [CrossRef] [Google Scholar]
  25. W.E. Warriner, C.A. Monroe, Locating solidification hot spots and feeder positions in casting geometries by image analysis, Int. J. Metalcast. 12 (2018) 224–234 [CrossRef] [Google Scholar]
  26. S.L. Nimbulkar, R.S. Dalu, Design optimization of gating and feeding system through simulation technique for sand casting of wear plate, Perspect. Sci. 8 (2016) 39–42 [CrossRef] [Google Scholar]
  27. M. Tiryakioğlu, E. Tiryakioğlu, A comparative study of optimum feeder models for castings, Int. J. Cast Metal. Res. 14 (2001) 25–30 [CrossRef] [Google Scholar]
  28. P.V. Kadam, B.S. Kamble, Optimization of feeder design using virtual simulation technique − a case study, Int. Res. J. Eng. Tech. 3 (2016) 1334–1339 [Google Scholar]
  29. B. Ravi, D. Joshi, Feedability analysis and optimisation driven by casting simulation, Indian Foundry J. 53 (2007) 71–78 [Google Scholar]
  30. F. Grosselle, G. Timelli, F. Bonollo, R. Molina, Correlation between microstructure and mechanical properties of Al-Si diecast engine blocks, Metall. Sci. Technol. 27 (2009) https://www.fracturae.com/index.php/MST/article/view/1140 [Google Scholar]
  31. Y. Birol, Impact of grain size on mechanical properties of AlSi7Mg0. 3 alloy, Mater. Sci. Eng. A 559 (2013) 394–400 [CrossRef] [Google Scholar]
  32. L. Ceschini, A. Morri, S. Toschi, S. Johansson, S. Seifeddine, Microstructural and mechanical properties characterization of heat treated and overaged cast A354 alloy with various SDAS at room and elevated temperature, Mater. Sci. Eng. A 648 (2015) 340–349 [CrossRef] [Google Scholar]
  33. A. Vergnano, U. Bergamini, D. Bianchi, P. Veronesi, R. Spagnolo, F. Leali, Simulation and experimental validation of Secondary Dendrite Arm Spacing for AlSi7Mg0.3 chassis parts in Low Pressure Die Casting, In: Advances on Mechanics, Design Engineering and Manufacturing III, Lect. Notes Mech. Eng. (2021) 28–33 [Google Scholar]
  34. L.A. Dobrzański, W. Borek, R. Maniara, Influence of the crystallization condition on Al-Si-Cu casting alloys structure, J. Achiev. Mater. Manuf. 18 (2006) 211–214 [Google Scholar]
  35. L.Y. Zhang, Y.H. Jiang, Z. Ma, S.F. Shan, Y.Z. Jia, C.Z. Fan, W.K. Wang, Effect of cooling rate on solidified microstructure and mechanical properties of aluminium-A356 alloy, J. Mater. Process. Tech. 207 (2008) 107–111 [CrossRef] [Google Scholar]
  36. A.F. Ferreira, J.A. Castro, L.D.O. Ferreira, Predicting secondary-dendrite arm spacing of the Al-4.5 wt% Cu alloy during unidirectional solidification, Mater. Res. 20 (2017) 68–75 [Google Scholar]
  37. J.H. Lee, H.S. Kim, S.I. Hong, C.W. Won, S.S. Cho, B.S. Chun, Effect of die geometry on the microstructure of indirect squeeze cast and gravity die cast 5083 wrought Al alloy and numerical analysis of the cooling behaviour, J. Mater. Process. Tech. 96 (1999) 188–197 [CrossRef] [Google Scholar]
  38. H. Yamagata, W. Kasprzak, M. Aniolek, H. Kurita, J.H. Sokolowski, The effect of average cooling rates on the microstructure of the Al-20% Si high pressure die casting alloy used for monolithic cylinder blocks, J. Mater. Process. Tech. 203 (2008) 333–341 [CrossRef] [Google Scholar]
  39. S. Farahany, M.H. Idris, A. Ourdjini, F. Faris, H. Ghandvar, Evaluation of the effect of grain refiners on the solidification characteristics of an Sr-modified ADC12 die-casting alloy by cooling curve thermal analysis, J. Therm. Anal. Calorim. 119 (2015) 1593–1601 [CrossRef] [Google Scholar]
  40. H. Hu, F. Chen, X. Chen, Y.L. Chu, P. Cheng, Effect of cooling water flow rates on local temperatures and heat transfer of casting dies, J. Mater. Process. Tech. 148 (2004) 57–67 [CrossRef] [Google Scholar]
  41. L. Zhang, L. Li, H. Ju, B. Zhu, Inverse identification of interfacial heat transfer coefficient between the casting and metal mold using neural network, Energy Convers. Manag. 51 (2010) 1898–1904 [CrossRef] [Google Scholar]
  42. A.N. Vasileiou, G.C. Vosniakos, D.I. Pantelis, On the feasibility of determining the heat transfer coefficient in casting simulations by genetic algorithms, Proc. Manuf. 11 (2017) 509–516 [Google Scholar]
  43. S. Pedrazzi, A. Vergnano, G. Allesina, P. Veronesi, F. Leali, P. Tartarini, A. Muscio, A simple test method for measurement of the interface thermal resistance of coated and uncoat-ed metal surfaces, J. Phys. Conf. Ser. 1599 (2020) 012049 [CrossRef] [Google Scholar]
  44. J.H. Lee, H.S. Kim, C.W. Won, B. Cantor, Effect of the gap distance on the cooling behavior and the microstructure of indirect squeeze cast and gravity die cast 5083 wrought Al alloy, Mater. Sci. Eng. A 338 (2002) 182–190 [CrossRef] [Google Scholar]
  45. P. Schwingenschlögl, P. Niederhofer, M. Merklein, Investigation on basic friction and wear mechanisms within hot stamping considering the influence of tool steel and hardness, Wear 426 (2019) 378–389 [CrossRef] [Google Scholar]
  46. P. Niederhofer, K. Eger, P. Schwingenschlögl, M. Merklein, Properties of tool steels for application in hot stamping, Steel Res. Int. 91 (2020) 1900422 [CrossRef] [Google Scholar]
  47. R.W. Lewis, K. Ravindran, Finite element simulation of metal casting, Int. J. Numer. Meth. Eng. 47 (2000) 29–59 [CrossRef] [Google Scholar]
  48. Z. Guo, N. Saunders, A.P. Miodownik, J.P. Schillé, Modelling of materials properties and behaviour critical to casting simulation. Mater. Sci. Eng. A 413 (2005) 465–469 [CrossRef] [Google Scholar]
  49. B. Ravi, Casting simulation and optimisation: benefits, bottlenecks and best practices, Indian Foundry J. 54 (2008) 47 [Google Scholar]
  50. K.C. Sarma, H. Adeli, Life‐cycle cost optimization of steel structures, Int. J. Numer. Meth. Eng. 55 (2002) 1451–1462 [CrossRef] [Google Scholar]
  51. C. Favi, M. Germani, M. Mandolini, Analytical cost estimation model in high pressure die casting, Procedia Manuf. 11 (2017) 526–535 [CrossRef] [Google Scholar]
  52. M.B. Ndaliman, P.A. Pius, Behavior of aluminum alloy castings under different pouring temperatures and speeds, Leonardo El. J. Pract. Technol. 6 (2007) 71–80 [Google Scholar]
  53. X.M. Zhang, W.P. Chen, Review on corrosion-wear resistance performance of materials in molten aluminum and its alloys, Trans. Nonferr. Metal. Soc. 25 (2015) 1715–1731 [CrossRef] [Google Scholar]
  54. ISO, UNI EN ISO 683-1: 2018 Heat-treatable steels, alloy steels and free-cutting steels [Google Scholar]
  55. Formadur® 2311 data sheet, Bonomi Acciai Srl, Lumezzane, Italy, accessed at https://www.bonomiacciai.it/wp-content/uploads/2021/09/Formadur%C2%AE-2311.pdf on April 29, 2022 [Google Scholar]
  56. D. Klobčar, J. Tušek, B. Taljat, Thermal fatigue of materials for die-casting tooling, Mater. Sci. Eng. A 472 (2008) 198–207 [CrossRef] [Google Scholar]
  57. S. Naimi, S.M. Hosseini, Tool steels in die-casting utilization and increased mold life, Adv. Mech. Eng. 7 (2015) 286071 [CrossRef] [Google Scholar]
  58. Thermodur® 2343 EFS Superclean data sheet, Deutsche Edelstahlwerke Specialty Steel GmbH & Co. KG, Witten, Germany, accessed at https://www.dew-stahl.com/fileadmin/files/dew-stahl.com/documents/Publikationen/Werkstoffdatenblaetter/Werkzeugstahl/Warmarbeitsstahl/GB_Thermodur2343.pdf on March 1, 2021 [Google Scholar]
  59. Thermodur® 2383 Supercool Product Brochure, Deutsche Edelstahlwerke Specialty Steel GmbH & Co. KG, Witten, Germany, accessed at https://www.dew-stahl.com/fileadmin/files/dew-stahl.com/documents/Publikationen/Broschueren/2020-004_DEW_Thermodur_2383_Supercool_EN.pdf on March 1, 2021 [Google Scholar]
  60. P. Niederhofer, F. van Soest, M. Gürcan, H.-G. Krull, T. Schneiders, Alternative alloying concepts of hot work tool steels for application in die casting, in Proceedings of the High Tech Die Casting (2021) [Google Scholar]
  61. A. Vergnano, E. Brambilla, G. Bonfiglioli, Efficiency and reliability of gravity die casting models for simulation based design. In: Advances on Mechanics, Design Engineering and Manufacturing II, Lect. Notes Mech. Eng. (2019), pp. 3–12, Cham, https://doi.org/10.1007/978-3-030-12346-8_1 [Google Scholar]
  62. A.J. Norwood, P.M. Dickens, R.C. Soar, R. Harris, G. Gibbons, R. Hansell, Analysis of cooling channels performance, Int. J. Comput. Integr. Manuf. 17 (2004) 669–678 [CrossRef] [Google Scholar]
  63. S. Yun, J. Kwon, W. Cho, D. Lee, Y. Kim, Performance improvement of hot stamping die for patchwork blank using mixed cooling channel designs with straight and conformal channels, Appl. Therm. Eng. 165 (2020) 114562 [CrossRef] [Google Scholar]
  64. S. Moayedinia, Quantification of cooling channel heat transfer in low pressure die casting, University of British Columbia (2014) [Google Scholar]
  65. H. Yavuz, O. Ertugrul, Numerical analysis of the cooling system performance and effectiveness in aluminum low-pressure die casting, Int. J. Metalcast. 15 (2020) 1–13 [Google Scholar]
  66. P.R. Anerao, Y.S. Munde, Thermal analysis of feeder neck using FEM for a metal casting, Int. J. Emerg. Technol. 2 (2012) 104–108 [Google Scholar]
  67. R. Tavakoli, P. Davami, Feeder growth: a new method for automatic optimal feeder design in gravity casting processes (2009) Struct. Multidiscip. O. 39 (2009) 519 [CrossRef] [Google Scholar]
  68. R. Monroe, Porosity in castings, Trans. Am. 113 (2005) 519–546 [Google Scholar]
  69. F. Peti, L. Grama, Analyze of the possible causes of porosity type defects in aluminium high pressure diecast parts, Scientific Bulletin of the“ Petru Maior” University of Targu Mures 8 (2011) 41–44 [Google Scholar]
  70. A. Carré, B. Böttger, M. Apel, Phase-field modelling of gas porosity formation during the solidification of aluminium, Int. J. Mater. Res. 101 (2010) 510–514 [CrossRef] [Google Scholar]
  71. P. Kotas, C. Tutum, J. Hattel, O. Šnajdrová, J. Thorborg, A casting yield optimization case study: Forging ram, Int. J. Metalcast. 4 (2010) 61–76 [CrossRef] [Google Scholar]
  72. U.S. Khade, S.M. Sawant, Gating design modification using 3D CAD modeling and casting simulation for improving the casting yield, Int. J. Adv. Mech. Eng. 4 (2014) 813–820 [Google Scholar]
  73. B. Chokkalingam, V. Raja, M. Dhineshkumar, M. Priya, R. Immanual, Energy Savings in Foundries through Yield Improvement and Defect Reduction in Castings, Arch. Foundry Eng. 18 (2018) 15–18 [Google Scholar]
  74. M.S.H. Riyaz, P.U. Raikar, Yield improvement of cast part using computer aided casting simulation, Int. Res. J. Eng. Technol. 2 (2015) 858–862 [Google Scholar]
  75. G.F. Vander Voort, J. Asensio-Lozano, The al-si phase diagram, Microsc. Microanal. 15 (2009) 60–61 [CrossRef] [Google Scholar]
  76. Magmasoft − MAGMA Casting Technology, www.magmasoft.de/en, accessed on March 1, 2021 [Google Scholar]

Cite this article as: Alberto Vergnano, Emanuele Salvati, Andrea Magistrelli, Edoardo Brambilla, Paolo Veronesi, Francesco Leali, A method for yield and cycle time improvements in Al alloy casting with enhanced conductivity steel for die construction, Manufacturing Rev. 9, 18 (2022)

All Tables

Table 1

CAD overall dimensions and mass properties.

In the text
Table 2

Materials selection for the die inserts in the design cases.

In the text
Table 3

Input variables, simulation and evaluation outputs for the six design cases.

In the text
Table 4

Cost estimation of the six design cases with respect to 1w design case.

In the text
Table 5

Production capacity of the six design cases.

In the text

All Figures

thumbnail Fig. 1

Method for yield and cycle time improvements through the evaluation of die designs with different layouts of steel cavity inserts and cooling channels.
In the text
thumbnail Fig. 2

Thermal conductivity of 1.2343 and 1.2383 steels [59,60].
In the text
thumbnail Fig. 3

Typical process phases in a die casting cycle.
In the text
thumbnail Fig. 4

CAD models of (a) the casting cavities and cores, of (b) the complete die and of (c) its inserts in an opened view.
In the text
thumbnail Fig. 5

Porosity occurrence result as simulated for the design case 3a before and after feeder optimization.
In the text
thumbnail Fig. 6

Solidification in the 3a optimized case at different (a), (b) and (c) time steps.
In the text
thumbnail Fig. 7

Simulation results for (a) the solidification time and (b) the SDAS in the combustion chambers of the engine head for case 3a.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.