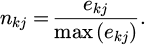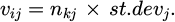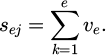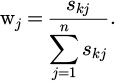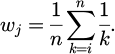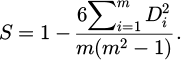| Issue |
Manufacturing Rev.
Volume 12, 2025
|
|
|---|---|---|
| Article Number | 16 | |
| Number of page(s) | 16 | |
| DOI | https://doi.org/10.1051/mfreview/2025014 | |
| Published online | 18 July 2025 | |
Original Article
A novel approach for determining criteria weights: application in ranking materials for mechanical manufacturing processes
School of Mechanical and Automotive Engineering, Hanoi University of Industry, CauDien, BacTuLiem, Hanoi, Vietnam
* e-mail: doductrung@haui.edu.vn
Received:
16
April
2025
Accepted:
23
June
2025
Material selection is a complex challenge within Multi-Criteria Decision-Making (MCDM). This research introduces SIWEC-ROC, a novel two-stage weighting method combining SIWEC and ROC to ensure stable material rankings across various MCDM techniques. The method first employs SIWEC to determine initial criterion weights and ranks, then applies ROC to calculate final weights based on these ranks. Validated across four mechanical engineering cases, including weighting for ranking gear materials, cutting tool materials, automotive protective plate materials, and EDM powders, SIWEC-ROC consistently demonstrated superior ranking stability compared to SIWEC alone. For example, average Spearman coefficients significantly improved: Case 1 showed 0.9563 for both SIWEC and SIWEC-ROC, Case 2 from 0.8368 to 0.9114, Case 3 from 0.8167 to 0.8667, and Case 4 from 0.8869 to 0.9212. The advantages of SIWEC-ROC over SIWEC were even clearer during sensitivity analysis. Using SIWEC-ROC allows engineers to quickly identify optimal materials, saving time, effort, and cost by reducing trial machining and boosting overall efficiency.
Key words: MCDM / weight method / SIWEC-ROC method / SIWEC method / ROC method / materials in mechanical manufacturing
© D. DucTrung et al., Published by EDP Sciences 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The ranking of material types represents a complex undertaking that has garnered significant attention from numerous researchers. This process necessitates the consideration of a multitude of parameters and is recognized as a multi-criteria decision-making (MCDM) problem. MCDM has not only been extensively employed for ranking materials for specific applications but also stands as a robust technique applicable across a wide array of domains, including personal and governmental policy, economics, and medicine, among others [1–4]. However, the resulting order of alternatives can vary depending on the specific MCDM method utilized [5, 6]. Consequently, several studies have indicated that employing multiple MCDM methods is crucial to ensure the reliability of the final outcomes [7]. Nevertheless, substantial discrepancies in the rankings obtained from different MCDM methods can still pose challenges for reaching a conclusive decision regarding the prioritization of alternatives. Key factors contributing to these variations include the inherent algorithms of different MCDM techniques, the data normalization procedures employed, and the methods used to determine the weights of the criteria [8–10].
Among these factors, the weights assigned to the criteria exert a substantial influence on the ranking of alternatives [11–13]. The weight of a criterion quantifies its relative importance compared to other criteria when collectively used to characterize the value of an object. Criteria weights can be established through objective, subjective, or integrated approaches [14, 15].
Numerous objective methods exist for determining criteria weights, including SMART [16], Entropy [17], LOPCOW [18], MEREC [19], and SPC [20], ect. These methods rely solely on mathematical formulations to derive the weights, notably disregarding expert opinions regarding the relative significance of the criteria [21]. This oversight can lead to suboptimal outcomes in MCDM problem-solving [22]. Furthermore, the performance of objective weighting methods in MCDM problems can vary considerably. For instance, a recent study reported that among three objective weighting methods—Entropy, MEREC, and SPC—Entropy exhibited the highest performance, followed by MEREC, with SPC demonstrating the lowest [23].
Subjective methods, in contrast, determine criteria weights based on the judgments of evaluators. Examples of such methods include AHP [24], RS [25], ROC [25], RR [25], and PIPRECIA [26], ect. When these methods are applied, the importance of criteria is assigned by the user. Consequently, the resulting weights are inherently dependent on the user’s experience and subjective assessments [27]. A lack of specialized knowledge or the presence of biases in the user’s judgments can lead to erroneous conclusions when employing subjective weights in MCDM problems [28, 29]. Moreover, a common characteristic of most subjective weighting methods is the necessity for pairwise comparisons of criteria. This can be challenging to ensure consistency across different experts and becomes increasingly difficult with a larger number of criteria per alternative [27, 28, 30], as the complexity of comparing each pair of criteria escalates [31–33]. Additionally, experts may find it difficult to articulate the rationale behind their pairwise comparisons [34]. Furthermore, subjective opinions tend to exhibit low repeatability, undermining transparency and accountability in the decision-making process [29]. Even a single decision-maker’s comparisons of criteria can vary over time [31]. It is also commonly observed that the performance of subjective weighting methods differs across MCDM problems, as evidenced by a recent study indicating that ROC and Lagrange outperformed RS [35].
The preceding brief overview highlights inherent limitations in both subjective and objective weighting methods. Despite this, some findings suggest that subjective methods are computationally simpler and easier to implement compared to objective approaches [31]. Furthermore, reports indicate that combined weights (derived from two or more methods) offer a suitable solution for diverse situations involving decision-making groups with varying levels of expertise [36], thus suggesting a research direction focused on integrating subjective weighting methods. However, the selection of subjective weighting methods for combination requires careful consideration, as more complex methods are prone to increased errors [37]. Another crucial point to consider when choosing subjective weighting methods for integration is that assigning weights to criteria using qualitative data can be influenced by the decision-maker’s preferences; therefore, employing numerical scales (quantitative data) is preferable to qualitative data [31, 38].
SIWEC represents a subjective method for determining criteria weights. However, it distinguishes itself from other subjective weighting methods in that users (experts) only need to evaluate the significance of the criteria without engaging in pairwise comparisons. It also employs quantitative data for criteria assessment [39]. Further details regarding this method will be provided in the subsequent section of this paper. Despite its recent online appearance in August 2024 (with the paper’s publication number dated December 2024), this method has rapidly attracted the attention of researchers for its application in determining criteria weights across various domains, including agri-food [40], sustainable agricultural tourism [41], unmanned aerial vehicle evaluation [42], and electric tractor assessment [43], ect. Given its notable advantages of requiring only the evaluation of criteria significance without pairwise comparisons and utilizing a quantitative measurement scale, the SIWEC method was selected for use in this research.
Another subjective weighting method based on the preferential ranking of criteria is the ROC method. ROC is recognized for its high accuracy (up to 96%) in selecting the best alternative [44]. A significant and established advantage of the ROC method is its ability to minimize errors associated with individual weights by identifying the “centroid of potential weights” while preserving the rank order of the objectives [44]. Numerous recent publications have also employed this method for determining criteria weights [44–47]. However, the application of the ROC method still requires users to define the preferential ranking among the parameters. This will be elaborated upon when describing the steps for applying the ROC method in the subsequent section of this paper. Clearly, the weights derived are heavily reliant on the decision-maker’s subjectivity [39], and this issue becomes more pronounced with a larger number of criteria [27, 28]. This leads to the idea that to leverage the benefits of the ROC method, it is still necessary to ensure the accuracy of the criteria’s importance when using ROC for weight determination. Stemming from this concept, the motivation for this research is to first calculate preliminary weights for the criteria to establish their preferential ranking, and then utilize the ROC method to compute the final weights. To determine these preliminary weights, this study employs the SIWEC method, the rationale for which lies in its advantages as previously discussed. The objective of this research is to propose a novel method for determining criteria weights. The proposed method is a combination of the SIWEC and ROC methods, denoted as the SIWEC-ROC method. The proposed SIWEC-ROC method holds significant potential for seamless integration into integrated design and manufacturing workflows. By providing a precise and reliable approach to criterion weighting, this method enables designers and engineers to easily quantify the importance of various material factors early in the product development cycle. This facilitates the selection of optimal materials based on specific performance, cost, and manufacturability requirements, thereby fostering a more efficient design process and mitigating manufacturing risks. The details of the proposed SIWEC-ROC method are presented in Section 2 of this paper. Examples of ranking materials used in mechanical manufacturing are provided in Section 3 to evaluate the effectiveness of the proposed method. In Section 4, the performance of the proposed method is further assessed through a sensitivity analysis. The final section concludes the research and outlines directions for future investigations.
2 Proposed methodology
To develop the SIWEC-ROC method, it is first necessary to outline the procedural steps for each constituent method: the SIWEC method and the ROC method.
The calculation of criteria weights using the SIWEC method follows these steps [39]:
– Determine the importance of each criterion by surveying experts. Let e be the number of experts consulted. This step yields a matrix as represented in Equation (1), where n is the number of criteria for each alternative, and ekj denotes the importance of criterion j as evaluated by expert k. Experts utilize a scale from 1 to 10 to assess the importance of the criteria.
– Normalize the matrix E using equation (2). It is important to note that the denominator in equation (2) represents the maximum importance value assigned to any criterion by any expert across all criteria.
– Compute the standard deviation of the importance scores for each criterion across all experts.
– Multiply the normalized values by their corresponding standard deviations according to equation (3).
– Calculate the aggregate weight for each criterion using equation (4).
– Determine the final weight of criterion j using equation (5).
To calculate criteria weights using the subjective ROC weighting method, the following steps are required [48,49]:
– Rank the criteria in descending order of preference, with the most important criterion assigned rank 1 and the least important criterion assigned rank n.
– Calculate the weight of each criterion using equation (6), where k is the rank of criterion j.
The SIWEC-ROC method represents a seamless integration of the SIWEC and ROC methods. The flowchart of the SIWEC-ROC method is illustrated in Figure 1. As depicted, the first six steps correspond to the determination of criteria weights using the SIWEC method. Subsequently, Step 7 involves establishing the rank order of the criteria based on their SIWEC weights. Following this, Step 8 applies the ROC method to calculate the final weights of the criteria. These ROC-derived weights constitute the output of the proposed methodology in this research, the SIWEC-ROC method.
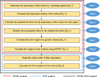 |
Fig. 1 Flowchart of the SIWEC-ROC method. |
3 Evaluating the effectiveness of the proposed method
To assess the efficacy of the SIWEC-ROC method, this section presents a comparative analysis between SIWEC-ROC and SIWEC. For this comparison, four distinct case studies concerning the ranking of four material groups in mechanical manufacturing were conducted. Given that the primary objective of this research is to propose the SIWEC-ROC method for criteria weighting, an in-depth analysis of material properties is not undertaken. Instead, for expediency, the data pertaining to the material types in each case were sourced from recently published articles. These four examples were intentionally selected to exhibit variations in the number of alternatives, the number and type of criteria, and the number of experts consulted in each case. This approach aims to provide a more objective evaluation of the effectiveness of the SIWEC-ROC method compared to the SIWEC method. The experts consulted in each case comprised experienced mechanical engineers in manufacturing and university professors with extensive teaching experience in mechanical processing disciplines. In each example, both the SIWEC-ROC and SIWEC methods were employed to determine the criteria weights. Subsequently, seven different MCDM methods—SAW, TOPSIS, MOORA, COPRAS, PIV, ROV, and RAM—were applied to rank the alternatives. A concise rationale for the selection of these seven MCDM methods follows: SAW is recognized as the simplest among MCDM techniques and serves as a foundational method for the development of others [50]. TOPSIS, MOORA, COPRAS, and ROV were included due to their widespread application and established prominence across various fields [51, 52]. PIV was chosen for its acknowledged advantage in mitigating rank reversal phenomena [53]. RAM was selected for its simplicity, relative novelty (introduced in September 2023), and its ability to balance positive and negative criteria [54]. Another noteworthy reason for employing these seven MCDM methods lies in the diversity of data normalization techniques they utilize. Specifically, SAW employs linear normalization, TOPSIS, MOORA, COPRAS, and PIV utilize vector normalization, ROV uses max-min linear normalization, and RAM employs linear sum normalization [51]. To compare SIWEC and SIWEC-ROC, the Spearman’s rank correlation coefficient was utilized. This coefficient reflects the similarity in the ranking order of alternatives when ranked by different MCDM methods and is calculated according to equation (7), where Di represents the difference in the rank of alternative i when ranked by different MCDM methods. A higher Spearman’s correlation coefficient value indicates greater rank stability of the alternatives, and vice versa [55, 56].
Case 1
This case study compares the application of SIWEC and SIWEC-ROC in ranking eight gear manufacturing materials, denoted MG1 to MG8, respectively. Each alternative is characterized by seven criteria, C1 to C7, as detailed in Table 1. Notably, only C7 is a cost-type criterion (smaller values are preferred), while the remaining six criteria are benefit-type (larger values are preferred) [57].
The process of determining criteria weights was executed as follows:
Six experts were consulted to evaluate the criteria, and their assessments are presented in Table 2.
Applying equations (2) through (5) yielded the criteria weights calculated using the SIWEC method, as summarized in Table 3. Consequently, the rank order of the criteria was established, as shown in the fourth row of this table. Based on this criteria ranking, equation (6) was applied to calculate the criteria weights using the ROC method, as presented in the fifth row of the same table. Since the criteria weights computed by the ROC method are based on the criteria ranking derived from the SIWEC method, this set of weights (the weights calculated by the ROC method) also represents the weight set generated by the SIWEC-ROC method in this study.
It is observed that while the criteria weights determined by the SIWEC-ROC method are derived from the SIWEC results, the proportional changes between the weights of these two methods are substantial. Specifically, using the SIWEC method, the ratio between the highest weight criterion, C1 (0.1965), and the lowest weight criterion, C7 (0.0883), is only 2.23 times. However, when employing the SIWEC-ROC method, the weight ratio of C1 to C7 is 18.16 times. This can be attributed to the SIWEC-ROC method’s reliance on the “centroid of potential weights” concept inherent in the ROC method [44].
Applying the SAW, TOPSIS, MOORA, COPRAS, PIV, ROV, and RAM methods resulted in the ranking of alternatives based on the two distinct weight sets calculated by the SIWEC and SIWEC-ROC methods, with the outcomes summarized in Table 4.
It is evident that the ranking of alternatives is not entirely consistent across different MCDM methods, nor when employing the two different weighting methods, SIWEC and SIWEC-ROC. This is a common occurrence in addressing MCDM problems and has been reported in numerous studies [4, 58]. To compare SIWEC and SIWEC-ROC, equation (6) was used to calculate the Spearman’s rank correlation coefficients between the MCDM methods, as summarized in Table 5.
The Spearman’s rank correlation coefficient values between each pair of MCDM methods are observed to be very high, close to 1. This indicates that regardless of whether SIWEC or SIWEC-ROC is used to determine the criteria weights, the ranking of the material types exhibits high stability when assessed by different MCDM methods. Furthermore, the average Spearman’s rank correlation coefficient across the MCDM methods when using the SIWEC-ROC method for criteria weighting (0.9563) is equivalent to that when using the SIWEC method (also 0.9563). Thus, in this specific case, the SIWEC-ROC method achieves comparable performance to the SIWEC method in terms of ranking stability across different MCDM techniques. This implies that both methods, when used for criteria weighting, generate sets of alternative rankings with similar levels of consistency across various MCDM approaches. However, a comprehensive conclusion regarding the comparison of SIWEC and SIWEC-ROC cannot be drawn solely based on one example; further comparisons across several other case studies are necessary.
Gear manufacturing material types.
Expert opinions on criteria in case 1.
Criteria weights in case 1 calculated by different methods.
Ranking of alternatives in case 1 by different MCDM methods.
Spearman’s rank correlation coefficients between MCDM methods in case 1.
Cutting tool material types.
Case 2
This case study involves a comparison between SIWEC and SIWEC-ROC in ranking twelve cutting tool materials (CTMs), denoted CTM1 to CTM12, respectively. Each CTM is characterized by seven criteria, C1 to C7, where only C4 is a cost-type criterion, and the remaining criteria are benefit-type, as in Table 6 [59].
In this case, seven experts were consulted to evaluate the criteria, and their opinions are[CE1] presented in Table 7.
The calculation of criteria weights using both the SIWEC and SIWEC-ROC methods was performed analogously to Case 1, with the results summarized in Table 8. It is observed that when the SIWEC method is used to determine criteria weights, the ratio between the highest weight criterion (C5) and the lowest weight criterion (C1) is 3.62 times. In contrast, this ratio is 18.16 times when the SIWEC-ROC method is employed. This difference can be explained similarly to Case 1, where the SIWEC-ROC method’s weight calculation is based on the “centroid of potential weights” concept of the ROC method.
The chart in Figure 2 illustrates the ranking of alternatives obtained by different MCDM methods for both scenarios: when criteria weights are calculated using SIWEC and when they are calculated using SIWEC-ROC. In the figure, the suffix “-S” appended to the MCDM method name indicates that the method was applied using criteria weights derived from the SIWEC method. For example, “SAW-S” signifies the application of the SAW method with SIWEC-derived weights, and “TOPSIS-S” indicates the use of the TOPSIS method with SIWEC-derived weights, and so forth. Similarly, the suffix “-ROC” appended to the MCDM method name indicates the use of criteria weights derived from the SIWEC-ROC method. For example, “MOORA-ROC” signifies the application of the MOORA method with SIWEC-ROC-derived weights, and “RAM-ROC” indicates the use of the RAM method with SIWEC-ROC-derived weights, and so forth.
Table 9 summarizes the Spearman’s rank correlation coefficients between the MCDM methods in this case. It is observed that the Spearman’s correlation coefficient between TOPSIS and MOORA is the lowest in both scenarios (SIWEC and SIWEC-ROC weighted criteria). However, when SIWEC is used for weighting, this value is 0.6364, whereas it increases to 0.8252 when SIWEC-ROC is used. This partially indicates that the SIWEC-ROC method achieves higher effectiveness than SIWEC in this case. Furthermore, the Spearman’s correlation coefficient between each pair of MCDM methods is consistently higher when criteria weights are determined using the SIWEC-ROC method compared to using the SIWEC method. This further suggests the superiority of SIWEC-ROC over SIWEC. Notably, the average Spearman’s rank correlation coefficient across the MCDM methods is significantly higher at 0.9114 when using SIWEC-ROC for criteria weighting, compared to 0.8368 when using SIWEC. This strongly affirms the enhanced performance of SIWEC-ROC over SIWEC in this specific case. This implies that when the SIWEC-ROC method is used for criteria weighting, the application of different MCDM methods to rank the alternatives yields sets of rankings with greater stability compared to using SIWEC for criteria weighting.
Thus, in the two cases examined, Case 1 showed comparable performance between the SIWEC and SIWEC-ROC methods, while Case 2 demonstrated the superior performance of the SIWEC-ROC method over SIWEC. Therefore, for a more thorough comparison of these two methods, further case studies involving other applications in ranking manufacturing materials for mechanical engineering are necessary.
Expert opinions on criteria in case 2.
Criteria weights in case 2 calculated by different methods.
 |
Fig. 2 Ranking of alternatives in case 2 by different methods. |
Spearman’s rank correlation coefficients between MCDM methods in case 2.
Case 3
This case study compares the SIWEC and SIWEC-ROC methods in the context of ranking five materials used for manufacturing car bumper protectors (MPPs), denoted MPP1 to MPP5 as presented in Table 10 [59]. Each MPP is characterized by six criteria, labeled C1 to C6, where C1 through C4 are benefit-type criteria, and C5 and C6 are cost-type criteria.
In this case, six experts were surveyed regarding their opinions on the criteria, and their responses are aggregated in Table 11.
The calculation of criteria weights using both the SIWEC and SIWEC-ROC methods was performed analogously to Case 1, with the resulting weights summarized in Table 12. In this case, the ratio between the highest weight criterion (C1) and the lowest weight criterion (C2) is 2.56 when using the SIWEC method and 14.69 when using the SIWEC-ROC method.
Figure 3 presents a compilation of the alternative rankings obtained by different MCDM methods for the two scenarios: criteria weights determined by SIWEC and by SIWEC-ROC. The Spearman’s rank correlation coefficients between the MCDM methods were also calculated and are summarized in Table 13.
The average Spearman’s rank correlation coefficient across the MCDM methods when using the SIWEC-ROC method for criteria weighting is observed to be 0.8667, which is notably higher than the 0.8167 obtained when using the SIWEC method. Thus, in this case, it can be concluded that employing the SIWEC-ROC method for criteria weighting ensures greater stability in the ranking order of the materials (when ranked by different MCDM methods) compared to using the SIWEC method. In essence, the SIWEC-ROC method demonstrates superior effectiveness over the SIWEC method in this instance. This also implies that when the SIWEC-ROC method is used to determine criteria weights, the application of various MCDM methods to rank the alternatives yields sets of rankings with higher consistency than when using the SIWEC method for criteria weighting.
Among the three cases conducted thus far, Case 1 indicated comparable performance between the SIWEC and SIWEC-ROC methods, while Case 2 and Case 3 demonstrated the superior effectiveness of SIWEC-ROC over SIWEC. Based on this, a preliminary observation suggests that SIWEC-ROC exhibits higher performance than SIWEC. However, to further substantiate this observation, it is necessary to conduct additional examples.
Decision matrix for case 3.
Expert opinions on criteria in case 3.
Criteria weights in case 3 calculated by different methods.
 |
Fig. 3 Ranking of alternatives in case 3 by different methods. |
Spearman's rank correlation coefficients between MCDM methods in case 3.
Case 4
This case study compares the SIWEC and SIWEC-ROC methods in the context of ranking ten powders used in the electrical discharge machining (EDM) process, denoted PM1 to PM10, respectively, as shown in Table 14 [60]. Each alternative is characterized by one cost-type criterion (criterion C1) and four benefit-type criteria (C2 to C5).
In this case, seven experts were surveyed regarding their opinions on the criteria, and their responses are aggregated in Table 15. The calculation of criteria weights using both the SIWEC and SIWEC-ROC methods was performed analogously to Case 1, with the resulting weights summarized in Table 16. In this case, the ratio between the highest weight criterion (C1) and the lowest weight criterion (C3) is 1.35 and 11.42 when using the SIWEC method and the SIWEC-ROC method, respectively.
Figure 4 illustrates the ranking of alternatives obtained by different MCDM methods for both scenarios: criteria weights determined by SIWEC and by SIWEC-ROC. The Spearman’s rank correlation coefficients between the MCDM methods were also calculated and are summarized in Table 17.
The average Spearman’s rank correlation coefficient across the MCDM methods is observed to be 0.9212 when using the SIWEC-ROC method for criteria weighting, which is higher than the 0.8869 obtained when using the SIWEC method. Thus, in this case, it is also concluded that the SIWEC-ROC method is more effective than the SIWEC method when used for determining criteria weights. Once again, it is reaffirmed that employing the SIWEC-ROC method for criteria weighting leads to more stable sets of alternative rankings when different MCDM methods are applied, compared to using the SIWEC method for criteria weighting.
After conducting the four cases above, some key information has been summarized in Table 18.
According to the information in Table 18, it is important to reiterate the numerous differences between the conducted cases, ranging from the number of alternatives to be ranked, the number of benefit-type criteria, the number of cost-type criteria, and the application domain. However, despite these variations, only Case 1 showed comparable effectiveness between the SIWEC and SIWEC-ROC methods in ensuring the stability of the alternatives' rankings when assessed by different MCDM methods. In the remaining three cases, the SIWEC-ROC method consistently demonstrated superior performance over the SIWEC method. In summary, it can be definitively concluded that using the SIWEC-ROC method for criteria weighting ensures greater stability in the ranking of alternatives when they are ranked by different MCDM methods, compared to using the SIWEC method for criteria weighting. Nevertheless, to finalize the comparison between the SIWEC-ROC and SIWEC methods, a sensitivity analysis is necessary. This content is presented in the subsequent section of this paper.
Decision matrix for case 4.
Expert opinions on criteria in case 4.
Criteria weights in case 4 calculated by different methods.
 |
Fig. 4 Ranking of alternatives in case 4 by different methods. |
Spearman’s rank correlation coefficients between MCDM methods in case 4.
Summary of information across the conducted cases.
4 Sensitivity analysis
To further ensure the objectivity of the comparison between the SIWEC and SIWEC-ROC methods, a sensitivity analysis was conducted for each case under varying scenarios. These scenarios were generated by systematically removing one alternative from the list of alternatives to be ranked. To maintain impartiality, the alternative selected for removal in each case was chosen randomly. Specifically, for Case 1, the first alternative (MG1) was removed; for Case 2, the last alternative (CTM12) was removed; for Case 3, the third alternative (MPP3) was removed; and for Case 4, the eighth alternative (PM8) was removed.
Figures 5, 6, 7 and 8 correspondingly illustrate the ranking of alternatives in each case after the removal of one alternative as described above. The average Spearman’s rank correlation coefficient between the MCDM methods in each case was also calculated and is summarized in Table 19.
The data in Table 19 indicate that even after randomly removing one alternative from the set of alternatives to be ranked in each case, the average Spearman’s rank correlation coefficient between the MCDM methods when using the SIWEC-ROC method for criteria weighting consistently remains higher than when using the SIWEC method. Notably, even in Case 1, where the average Spearman’s correlation coefficient was equal for both methods before removing MG1 (refer back to Tab. 5), SIWEC-ROC demonstrates an advantage over SIWEC after the removal of MG1. Thus, this sensitivity analysis reveals that across all four cases, employing the SIWEC-ROC method for criteria weighting ensures greater stability in the ranking of the alternatives (material types) when assessed by different MCDM methods compared to using the SIWEC method. This outcome can be attributed to the fact that the SIWEC-ROC method’s reliance on the “centroid of potential weights” concept from the ROC method results in a significantly larger ratio between the highest and lowest criteria weights compared to the SIWEC method.
In summary, the findings from Sections 3 and 4 lead to a robust conclusion: utilizing the SIWEC-ROC method for determining criteria weights enhances the stability of the alternatives' rankings when evaluated using different MCDM methods to a greater extent than employing the SIWEC method. By utilizing the SIWEC-ROC method for criterion weighting, engineers can quickly and accurately determine the optimal ranking of materials for specific applications. This ranking fully incorporates the consensus of all mechanical engineering experts regarding the importance of various criteria, leading to the selection of the best materials. This, in turn, significantly reduces testing time, lowers trial machining costs, minimizes scrap rates, and ultimately enhances the overall efficiency of the product manufacturing process and the in-use performance of finished products.
 |
Fig. 5 Ranking of alternatives in case 1 after removing MG1. |
 |
Fig. 6 Ranking of alternatives in case 2 after removing CTM12. |
 |
Fig. 7 Ranking of alternatives in case 3 after removing MPP3. |
 |
Fig. 8 Ranking of alternatives in case 4 after removing PM8. |
Average Spearman’s rank correlation coefficients between MCDM methods.
5 Conclusion
A novel method for determining criteria weights, termed SIWEC-ROC, has been proposed in this research. This method integrates the SIWEC and ROC approaches. A comparative analysis between SIWEC and SIWEC-ROC was conducted through four illustrative examples pertaining to the ranking of materials in mechanical manufacturing. These examples exhibited variations in the number of alternatives to be ranked, the number of benefit-type criteria, the number of cost-type criteria, and the number of experts consulted for criteria evaluation. Furthermore, the comparison was extended to a sensitivity analysis phase. Across all conducted analyses, the SIWEC-ROC method consistently yielded a higher average Spearman’s rank correlation coefficient among the MCDM methods used for ranking the alternatives compared to when the SIWEC method was employed for criteria weighting. Specifically, when calculating the weights for criteria of gear manufacturing materials, the average Spearman’s coefficient value is consistently 0.9563 for both cases using the SIWEC and SIWEC-ROC methods to determine criterion weights. For calculating the weights of cutting tool material criteria, the average Spearman’s coefficient is 0.8368 when using the SIWEC method, and it increases to 0.9114 when using the SIWEC-ROC method. When determining weights for automotive protective plate material criteria, the average Spearman’s coefficient is 0.8167 with the SIWEC method, and it becomes 0.8667 with the SIWEC-ROC method. In the fourth case, for EDM powder material criteria, the average Spearman’s coefficient is 0.8869 using the SIWEC method, and it increases to 0.9212 with the SIWEC-ROC method. The advantages of the SIWEC-ROC method over the original SIWEC method are even more pronounced during the sensitivity analysis phase. In this phase, the average Spearman’s coefficient between MCDM methods across the four examples are 0.9048, 0.8909, 0.9333, and 0.9722, respectively, when using the SIWEC-ROC method to weight the criteria. In contrast, when using the original SIWEC method to weight the criteria, the corresponding values for each example are 0.8929, 0.8227, 0.8000, and 0.9278.
By utilizing the SIWEC-ROC method for criterion weighting, engineers can quickly and accurately determine the precise ranking of materials for each specific application. This not only saves time and costs by eliminating the need for trial machining processes but also contributes to improving the quality of product usage from both technical and economic perspectives.
In summary, this research suggests that the SIWEC-ROC method should be used for criterion weighting instead of the SIWEC method.
The comparative analysis between SIWEC-ROC and SIWEC in this study has been limited to four cases within the domain of material ranking for mechanical manufacturing. Future research could explore the performance of SIWEC-ROC and SIWEC in other application areas. Additionally, future experimental validation of the proposed method’s application is needed to firmly establish its advantages and demonstrate its potential for improving manufacturing process performance.
Funding
This research received no external funding.
Conflicts of interest
The authors declare no conflict of interest.
Data availability statement
Data sets generated during the current study are available from the corresponding author on reasonable request.
Author contribution statement
Do Duc Trung: conceptualisation, literature review, methodology, resources, writing—original draft preparation, analysis, review, writing—original draft preparation. Hoang Tien Dung: resources, analysis, visualisation, resources, supervision and validation. Nguyen Chi Bao: review the data, analysis. Duong Van Duc review citation, analysis and validation.
References
- M.H. Alamoudi, O.A. Bafail, BWM-RAPS approach for evaluating and ranking banking sector companies based on their financial indicators in the Saudi stock market, J. Risk Financial Manag. 15 (2022) 1–20 [Google Scholar]
- M. Mohammadi, J. Rezaei, Ratio product model: A rank-preserving normalization-agnostic multicriteria decision-making method, J. Multi-Crit. Decis. Anal. 30 (2023) 163–172 [Google Scholar]
- M. Nuriyev, Z-numbers based hybrid MCDM approach for energy resources ranking and selection, Int. J. Energy Econ. Policy 10 (2020) 22–30 [Google Scholar]
- D.T. Do, Assessing the impact of criterion weights on the ranking of the top ten universities in Vietnam, engineering, Technol. Appl. Sci. Res. 14 (2024) 14899–14903 [Google Scholar]
- E. Vassoney, A.M. Mochet, E. Desiderio, G. Negro, M.G. Pilloni, C. Comoglio, Comparing multi-criteria decision making methods for the assessment of flow release scenarios from small hydropower plants in the alpine area, Front. Environ[CE1]. Sci. 8 (2021) [Google Scholar]
- R.K. Dhurkari, MCDM METHODS: Practical difficulties and future directions for improvement, RAIRO-Oper. Res. 56 (2022) 2221–2233 [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- M.A. Fattouh, A.S. Eisa, The Significance of weighting in multicriteria decision-making methods: a case study on robot selection, Eng. Res. J. Faculty Eng. Menoufia Univ. 46 (2023) 339–352 [Google Scholar]
- A.D.A. Mandil, M.M. Salih, Y.R. Muhsen, Opinion weight criteria method (OWCM): A new method for weighting criteria with zero inconsistency, IEEE Access 12 (2024) 5605–5616 [Google Scholar]
- E. Roszkowska, The extension of rank ordering criteria weighting methods in fuzzy environment, Oper. Res. decis. 2020 (2020) 91–114 [Google Scholar]
- S. Zakeri, P. Chatterjee, D. Konstantas, F. Ecer, A decision analysis model for material selection using simple ranking process, Sci. Rep. 13 (2023) [Google Scholar]
- C. Kao, Weight determination for consistently ranking alternatives in multiple criteria decision analysis, Appl. Math. Model. 34 (2010) 1779–1787 [Google Scholar]
- M. Soltanifa, A new interval for ranking alternatives in multi attribute decision making problems, J. Appl. Res. Ind. Eng. 11 (2024) 37–56 [Google Scholar]
- Y. Dorfeshan, R.T. Moghaddam, F. Jolai, S.M. Mousav, A new grey decision model-based reference point method for decision makers and criteria’s weight, and final ranking, J. Ind. Syst. Eng. 14 (2022) 284–297 [Google Scholar]
- M.A. Hatefi, An improved rank order centroid method (IROC) for criteria weight estimation: an application in the engine/vehicle selection problem, Informatica 34 (2023) 249–270 [Google Scholar]
- Y. Omari, D. Hamdadou, M.A. Mami, Assigning decision makers’ weights using topsis method in spatial multicriteria group decision support system, J. Posit. School Psychol. 6 (2022) 8602–8609 [Google Scholar]
- J.J Thakkar, Stepwise weight assessment ratio analysis (SWARA), in: Multi-Criteria Decision Making. Studies in Systems, Decision and Control, 336, (2021) [Google Scholar]
- D.D. Trung, H.X. Thinh, A multi-criteria decision-making in turning process using the MAIRCA, EAMR, MARCOS and TOPSIS methods: A comparative study, Adv. Produc. Eng. Manag. 16 (2021) 443–456 [Google Scholar]
- F. Ecer, D. Pamucar, A novel LOPCOW-DOBI multi-criteria sustainability performance assessment methodology: An application in developing country banking sector, Omega 112 (2022) [Google Scholar]
- M. Keshavarz-Ghorabaee, M. Amiri, E.K. Zavadskas, Z. Turskis, J. Antucheviciene, Determination of objective weights using a new method based on the removal effects of criteria (MEREC), Symmetry 13 (2021) [Google Scholar]
- Z. Gligoric, M. Gligoric, I. Miljanovic, S. Lutovac, A. Milutinovic, Assessing criteria weights by the symmetry point of criterion (Novel SPC Method)–application in the efciency evaluation of the mineral deposit multi-criteria partitioning algorithm, Comput. Model. Eng. Sci. 136 (2023) [Google Scholar]
- A.R. Paramanik, S. Sarkar, B. Sarkar, OSWMI: An objective-subjective weighted method for minimizing inconsistency in multi-criteria decision making, Comput&. Ind. Eng. 169 (2022) [Google Scholar]
- V. Podvezko, E.K. Zavadskas, A. Podviezko, An extension of the new objective weight assessment methods CILOS and IDOCRIW to fuzzy MCDM, Econ. Comput. Econ. Cybern. Stud. Res. 2020 (2020) 59–75 [Google Scholar]
- N.T.D. Linh, N.H. Son, D.X. Thao, Evaluating the impact of weighting methods on the stability of scores for alternatives in multicriteria decision-making problems, Eng. Technol&. Appl. Sci. Res. 15 (2025) 19998–20004 [Google Scholar]
- F. Cai, Z. Hu, B. Jiang, W. Ruan, S. Cai, H. Zou, Ecological health assessment with the combination weight method for the river reach after the retirement and renovation of small hydropower stations, Water 15 (2023) [Google Scholar]
- M. Danielson, L. Ekenberg, A robustness study of state-of-the-art surrogate weights for MCDM, Group DecisNegot 26 (2017) 677–691 [Google Scholar]
- D.D. Trung, N.X. Truong, H.X. Thinh, Combined PIPRECIA method and modified FUCA method for selection of lathe, J. Appl. Eng. Sci. 20 (2022) 1355–1365 [Google Scholar]
- S. Zakeri, D. Konstantas, P. Chatterjee, E.K. Zavadskas, Soft cluster-rectangle method for eliciting criteria weights in multicriteria decision-making, Sci. Rep. 15 (2025) [Google Scholar]
- H.–-J. Shyur, Combination weighting method using Z-numbers for multi-criteria decision-making, Appl. Soft. Comput. 174 (2025) [Google Scholar]
- H. Sulistiani, Setiawansyah, A.F.O. Pasaribu, P. Palupiningsih, K. Anwar, V.H. Saputra, New TOPSIS: modification of the TOPSIS method for objective determination of weighting, Int. J. Intell. Eng. Syst. 17 (2024) 991–1003 [Google Scholar]
- L.V. Cremades, A. Ponsich, Simple and objective determination of criteria weights for evaluating alternatives when using the analytic hierarchy process, IJAHP 16 (2024) 1–24 [Google Scholar]
- G.O. Odu, Weighting methods for multi-criteria decision making technique, J. Appl. Sci. Environ. Manag. 23 (2019) 1449–1457 [Google Scholar]
- S. Lakmayer, M. Danielson, Effcient weight ranking in multi-criteria decision support systems, Electronics 14 (2025) [Google Scholar]
- H.K. Alfares, S.O. Du®uaa, Simulation-based evaluation of criteria rank-weighting methods in multi-criteria decision-making, Int. J. Inf. Technol. Decis. Mak. 15 (2016) [Google Scholar]
- M. Qiyas, T. Madrar, S. Khan, S. Abdullah, T. Botmart, A. Jirawattanapaint, Decision support system based on fuzzy credibility Dombi aggregation operators and modified TOPSIS method, AIMS Math. 7 (2022) 19057–19082 [Google Scholar]
- N.T. Giang, H.X. Thinh, N.T. Giang, Comparing subjective weighting methods in multi-criteria decision-making: an application to electric bicycle ranking, engineering, Technol. Appl. Sci. Res. 15 (2025) 21963–21969 [Google Scholar]
- M. Alemi-Ardakani, A.S. Milani, S. Yannacopoulos, G. Shokouhi, On the effect of subjective, objective and combinative weighting in multiple criteria decision making: A case study on impact optimization of composites, Expert Syst. Appl. 46 (2016) 426–438 [Google Scholar]
- B. Nemeth, A. Molnar, S. Bozoki, K. Wijaya, A. Inotai, J.D. Campbell, Z. Kalo, Comparison of weighting methods used in multicriteria decision analysis frameworks in healthcare with focus on low- and middle-income countries, J. Comp. Effect. Res. 8 (2019) 195–204 [Google Scholar]
- T.L. Saaty, A scaling method for priorities inheirachical structures, J. Math. Psychol. 15 (1977) 234–281 [CrossRef] [Google Scholar]
- A. Puška, M. Nedeljković, D. Pamučar, D. Božanić, V. Simić, Application of the new simple weight calculation (SIWEC) method in the case study in the sales channels of agricultural products, MethodsX 13 (2024) [Google Scholar]
- M. Nedeljković, Z. Papović, S. Krstić, Assessment of the weight of factors influencing food losses using fuzzy multi-criteria analysis, Econ. Agric. 71 (2024) 1313–1324 [Google Scholar]
- M. Nedeljkovic, S. Vujičić, Evaluation of sustainable agricultural tourism criteria, Climate changes and ecological sustainability in agriculture and food production in Serbia, the region and Southeastern Europe: proceedings 2025 (2025) 250–256 [Google Scholar]
- A. Puška, M. Nedeljković, D. Božanic, A. Štilić, Y.R. Muhsen, Evaluation of agricultural drones based on the compromise ranking from alternative solutions (CORASO) methodology, Eng. Rev. 2024 (2024) 77–90 [Google Scholar]
- A. Puška, D. Božanić, A. Štilić, M. Nedeljković, M. Khalilzadeh, Application of fuzzy-rough methodology to the selection of electric tractors for small farms in Semberija, J. Fuzzy Ext. Appl. (2025) [Google Scholar]
- T. Varshney, A.V. Waghmare, V.P. Singh, M. Ramu, N. Patnana, V.P. Meena, A.T. Azar, I.A. Hameed, Investigation of rank order centroid method for optimal generation control, Sci. Rep. 14 (2024) Art. no. 11267 [Google Scholar]
- H.X. Thinh, Multi-objective optimization of turning process by FUCA method, Strojníckyčasopis, J. Mech. Eng. 73 (2023) 55–66 [Google Scholar]
- D.D. Trung, Application of TOPSIS and PIV methods for multi-criteria decision making in hard turning process, J. Mach. Eng. 21 (2021) 57–71 [CrossRef] [Google Scholar]
- D.D. Trung, N. Nhu-Tung, Applying COCOSO, MABAC, MAIRCA, EAMR, TOPSIS and weight determination methods for multi-criteria decision making in hole turning process, Strojníckyčasopis, J. Mech. Eng. 72 (2022) 15–40 [Google Scholar]
- B. Ahcène, A new method for determining the weights in multi-criteria decision making based on ordinal ranking of criteria and lagrange multiplier, Metall. Min. Ind. 5 (2017) 22–31 [Google Scholar]
- M. Bouhedja, S. Bouhedja, A. Benselhoub, Testing the suitability of vector normalization procedure in TOPSIS method: Application to wheel loader selection, Math. Model. 2 (2024) 52–62 [Google Scholar]
- T.V. Huy, N.Q. Quyet, V.H. Binh, T.M. Hoang, N.T.T. Tien, L.T. Anh, D.T. Nga, N.Q. Doan, P.H. Tu, D.D. Trung, Multi-criteria decision-making for electric bicycle selection, Adv. Eng. Lett. 1 (2022) 126–135 [Google Scholar]
- D.D. Trung, Application of TOPSIS and PIV methods for multi-criteria decision making in hard turning process, J. Mach. Eng. 21 (2021) 57–71 [CrossRef] [Google Scholar]
- D.H. Tien, D.D. Trung, N.V. Thien, Comparison of multi-criteria decision making methods using the same data standardization method, Strojníckyčasopis, J. Mech. Eng. 72 (2022) 57–72 [Google Scholar]
- S. Mufazzal, S.M. Muzakkir, A new multi-criterion decision making (MCDM) method based on proximity indexed value for minimizing rank reversals, Comput&. Ind. Eng. 119 (2018) 427–438 [Google Scholar]
- A.S. Anvari, Root assessment method (RAM): A novel multi-criteria decision making method and its applications in sustainability challenges, J. Clean. Prod. 423 (2023) [Google Scholar]
- B. Kizielewicz, A. Baczkiewicz, Comparison of Fuzzy TOPSIS, Fuzzy VIKOR, Fuzzy WASPAS and Fuzzy MMOORA methods in the housing selection problem, Proc. Comput. Sci. 192 (2021) 4578–4591 [Google Scholar]
- P. Aazagreyir, P. Appiahene, O. Appiah, S. Boateng, Comparative analysis of fuzzy multi-criteria decision-making methods for quality of service-based web service selection, IAES Int. J. Artif. Intell. 13 (2024) 1408–1419 [Google Scholar]
- H.X. Thinh, T.V. Dua, Research on expanding the scope of application of the MARA method, EUREKA: Phys. Eng. 2024 (2024) 90–99 [Google Scholar]
- S. Bošković, L. Švadlenka, S. Jovčić, M. Dobrodolac, V. Simić, N. Bacanin, An alternative ranking order method accounting for two step normalization (AROMAN)—A case study of the electric vehicle selection problem, IEEE Access 11 (2023) 39496–39507 [Google Scholar]
- T. Van Dua, Application of the collaborative unbiased rank list integration method to select the materials, Appl. Eng. Lett. 7 (2022) 133–142 [Google Scholar]
- N.V. Thien, N.H. Son, Material selection for PMEDM process, Int. J. Mech. Eng. Robot. Res. 13 (2024) 315–324 [Google Scholar]
Cite this article as: Do Duc Trung, Hoang Tien Dung, Nguyen Chi Bao, Duong Van Duc, A novel approach for determining criteria weights: application in ranking materials for mechanical manufacturing processes, Manufacturing Rev. 12, 16 (2025), https://10.1051/mfreview/2025014
All Tables
All Figures
 |
Fig. 1 Flowchart of the SIWEC-ROC method. |
| In the text | |
 |
Fig. 2 Ranking of alternatives in case 2 by different methods. |
| In the text | |
 |
Fig. 3 Ranking of alternatives in case 3 by different methods. |
| In the text | |
 |
Fig. 4 Ranking of alternatives in case 4 by different methods. |
| In the text | |
 |
Fig. 5 Ranking of alternatives in case 1 after removing MG1. |
| In the text | |
 |
Fig. 6 Ranking of alternatives in case 2 after removing CTM12. |
| In the text | |
 |
Fig. 7 Ranking of alternatives in case 3 after removing MPP3. |
| In the text | |
 |
Fig. 8 Ranking of alternatives in case 4 after removing PM8. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.