EDP Sciences logo
Submit your paper
Search
Menu
Home All issues Volume 1 (2014) Manufacturing Rev., 1 (2014) 6 Full HTML
Open Access
Review
Issue
Manufacturing Rev.
Volume 1, 2014
Article Number 6
Number of page(s) 21
DOI https://doi.org/10.1051/mfreview/2014006
Published online 05 August 2014

© F. Chen et al., Published by EDP Sciences, 2014

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

Hot forging can serve to tailor the service properties of metals through microstructure evolution, in addition to altering their shape [1, 2]. On the one hand, an optimal design scheme for hot forging must ensure the required shape and size; on the other hand, the most important issue in forging is that the forging scheme must meet the parts made in respect of their performance requirements such as strength and toughness as well as resistance to corrosion, etc., of high temperature parts, as well as the high-temperature tensile properties of performance, creep resistance and thermal fatigue properties. Metallography has indicated that grain size has a decisive effect on the above mechanical properties of the forgings after the chemical composition of the specific raw material has been determined, with regard to such as large power-station turbine rotors [3] and aeronautical blades [4]. In most metals and alloys, the grain size of forgings are mainly determined by forging and heat-treating processes, where a fine-grained microstructure produced by forging plays a key role in obtaining a fine-grained microstructure in the following heat-treatment process. Therefore, study of microstructural evolution during the forging process, and furthermore, prediction of the grain-size distribution of forgings, have important practical significance. This has become a very important consideration in the design and optimization of a forging scheme: it is also the cutting edge research in the field of thermal processing and significantly affects the future developments in this field.

Generally, hot forging is often classified according to the forging equipment and how the forging operation is performed, i.e. by die forging or free forging. Microstructural evolution during die forging is mainly dominated by the following two steps: heating and single-hit deformation. In the heating process, the heating temperature, heating rate and holding time tremendously influence the grain evolution. For single-hit deformation, dynamic recrystallization (DRX), which affects the grain-size distribution of the final forging for metals with moderate-to-low stacking fault energy, plays a dominant role in the microstructural evolution at elevated temperature. Over the past half century, a number of research groups have attempted to secure better understanding and controlling of the grain evolution for various metal and alloys during heating and DRX, and a series of phenomenological models have also been developed to predict grain evolution during heating and DRX [5–29]. In recent years, with the rapid development of computer technology, mesosopic models have also been proposed to predict microstructural evolution during DRX. In distinct comparison to die forging, multi-hitting and multi-heating are the typical characteristics of free forging, such as in the production of heavy forgings, during which DRX, static recrystallization (SRX) and meta-dynamic recrystallization (MDRX) are important microstructural evolution mechanisms. The hot-deformed grains exhibit a quite different and more complex recrystallization behavior than that for single-blow deformed grains. In order to predict grain evolution during complex recrystallization processes, many empirical, semi-theoretical and mesocopic models for the grain evolution have been proposed by metallurgical and material researchers. Among these models, the phenomenological model that describes the relationship of austenite grain size with temperature, strain and strain-rate have been used practically [5, 6]. At the same time, with the use of the finite-element (FE) method, simulations coupled with the developed phenomenological models assumed a prominent role in investigation of the processing parameters such as temperature, strain and strain-rate.

The following mainly presents a critical review of the methods for the prediction of microstructural evolution during the hot-forging process. Generally speaking, the methods are mainly divided into the following four categories:

  1. Phenomenological model. This expresses mathematically the results of observed phenomena without paying detailed attention to their fundamental significance. In other words, the phenomenological model lacks a physical background that accounts for experimental observations. Additionally, the coefficients in the model are obtained by a regression method based on extensive experimental observations [5–42]. As a result, the model can only be used within a specified range, otherwise the use of the model beyond the range of the sample data is likely to result in serious error. Therefore, it is imperative to update the model parameters based on the details of the hot-forging scheme employed.

  2. Physically-based on internal variable model. This accounts for physical aspects of the material behaviour, such as the constitutive behaviour and the dynamic microstructural development in the hot working of metals and alloys [43–45]. According to different scale lengths (SL), grain size, volume fraction of different types of grain, volume fraction of phases, sub-grain size, second-phase particles and dislocation density can be used as the mesoscale and microscale internal state variables (ISVs) [46–59]. It is worth noting that the ISVs are independent of each other, and therefore the flow stress cannot serve as the ISV, because the flow stress mainly depends on the evolution of the microstructure. Generally, compared to the phenomenological descriptions, these models allow for an accurate definition of material behaviour under wide ranges of loading conditions by some physical assumptions and a larger number of materials constants. Most internal-variable-based constitutive models are completely capable of describing strain-hardening and dynamic recovery. However, one of the main disadvantages of this approach is that they are often not so well suited to the capture of minor alloying differences, phase transformations, or recrystallization phenomena [46].

  3. Mesoscale modelling. According to their differences in physical methodology and numerical algorithms, the mesoscopic modelling tools are explicitly grouped into different categories, e.g., the Monte Carlo (MC) model, the Cellular Automaton (CA) model, vertex models and phase-field (PF) models. These methods can not only successfully provide the general average microstructure properties, but can also model the evolution of the grains [60, 61]. The common characteristic of all these models is that they try to use just one basic physical concept to summarize the different microstructural evolution phenomena [62]. A representative example is the cellular automate (CA) models, which are algorithms that describe the discrete spatial and temporal evolution of complex systems by applying local deterministic or probabilistic transformation rules to the cells of a regular (or non-regular) lattice [63]. Mostly such models are not always so much thermodynamically based but rather rooting in corresponding simple local mobility and driving-force rules as well as local rules that systematically act on the neighbouring cells. The CA method of using each cell as a little automaton makes this method relatively efficient and fast. These features indicate that it is possible to model the microstructure evolution within a unified frame [64–66]. In contrast to the limited applicability of the macro-scale models, e.g., the phenomenological model and the statistical model, this characteristic of mesoscopic models also shows the latent advantage of the numerical solution of the complexity of microstructural evolution globally [60–103], such as normal grain growth [68–76], recrystallization [82–98] and phase transformation [100–103].

  4. Advanced statistical model. The artificial neural network (ANN) model is a typical statistical model [104]. During the hot forging of metals and alloys, the microstructural evolution involves complex, dynamic and often non-linear processes. The final grain size of forgings is highly sensitive to processing parameters, such as temperature, strain and strain rate, whilst at the same time many factors affecting the grain size are also non-linear. The accuracy of grain size predicted by a phenomenological model, the model constants of which are obtained by a regression method, is low and is applicable within only a limited range of measurable parameters. The artificial neural network is an information-treatment system with the characteristics of adaptive learning. It is especially suitable for treating non-linear phenomena and complex relationships and has been applied successfully to the prediction and control of non-linear systems and systems with unknown models [105, 106]. Generally, one of the main advantages of this approach is that it is not necessary to postulate an initial mathematical model (delete at first) or identify its parameters using an artificial neural network [107–114]. The main disadvantage of the statistical model is that this method does not provide a reasonable explanation for the physical meaning of the model.

2 Phenomenological model

Phenomenological models are widely used in the simulation of the forging processes of metals and alloys. The common features of phenomenological models are that the recrystallized fraction and grain size can be expressed as functions of the process parameters (strain, strain-rate and temperature) to consider the effects of these forming parameters on the microstructural evolution of metals and alloys. Until now, these have also been combined within more complex thermal and mechanical models, e.g., various FEM codes. The modelling interactions are illustrated in Figure 1.

thumbnail Figure 1.

Schematic diagram showing the use of the phenomenology model in hot forging processes.

2.1 Developments in phenomenological modelling

Sellars and co-workers [7] considered the different microscopic phenomena e.g., dynamic recrystallization, static recrystallization, metadynamic recrystallization and grain growth, and provided algorithms for calculating the recrystallized fraction, grain size and grain boundary area for the first time. Figure 2 shows the diagram of the algorithm used by Sellars et al. [7, 8]. At the same time, these authors gave the evolution equations for low-carbon steels, and developed a set of phenomenological models relating important metallurgical variables to the Zener-Hollomon parameter, time, and temperature and grain-size, as shown in Table 1. Generally, the typical characteristics of the Sellars model is the introduction of the constant (0.693) in the kinetic equation, which results in clear physical significance and simple calculation. Subsequently, the time-variable form was also used in the recrystallization kinetic equation of the McQueen model [9].

thumbnail Figure 2.

The flow chart of the technical routing of Sellars methodology.
Table 1.

Sellars model for different microscopic phenomena in hot working of C-Mn steel.

Yada et al. [10] proposed using a strain-variable form of the dynamic recrystallization kinetic equation for the first time, expressed by the following equation for a low C-Mn steel, as shown in Table 2.

Table 2.

Yada model for different microscopic phenomena in hot working of C-Mn steel.

Based on the above review, the following is a summary of the main points of these two typical phenomenological models:

  1. The kinetic equation of dynamic recrystallization. Although the different variables used in the Yada model and the Sellars model, i.e., the Sellars model is a function of time and the Yada model is a function of strain, both of them are the same in nature. This is because the function of time is consistent with the function of strain when the strain rate is constant. Thus, the Yada model can be applied to unsteady numerical simulations during hot deformation as a result of the use of the strain form. Therefore, many kinds of commercial FEM software, such as Deform, Superform and Marc, employ the Yada model to predict microstructural evolution. Differently from the Sellars model, the physical meaning of the variable ε0.5 in the Yada model is not obvious, and no longer precisely represents the strain for 50% DRX, but is just a statistic: it is difficult to determine the value of ε0.5. Apart from this, the difference between the Sellars model and the Yada model is that the value of the exponent used in the Sellars model is 1, whilst in the Yada model it is 2.

  2. The kinetic equation of static recrystallization. Although the time-variable form is used in both the Yada model and the Sellars model, the effect of strain rate on the static recrystallization volume-fraction was introduced in the Yada model. Furthermore, by employing the variable SV, i.e., the grain boundary area per unit volume, into the calculation model of t0.5, the effects of initial grain size and deformation degree on the static recrystallization behavior were introduced, which make the physical meaning of the model more obvious.

To date, Kopp et al. [11], Laasraoui and Jonas [12], Nanba et al. [13], Hodgson et al. [14], Kim et al. [15, 16], Serajzadeh and Taheri [17], Liu et al. [18] and Dehghan-Manshadi et al. [19] have enriched the phenomenological models which are used in the prediction of microstructural evolution during hot deformation for metals and alloys. Furthermore, many researchers have integrated the developed phenomenological models into FEM to predict the microstructural evolution during hot forging [20–29]. Jang et al. [20] investigated the microstructural evolution during a hot-forging process of C-Mn steel with large deformation by combining a recrystallization model and the rigid-thermoviscoplastic finite-element method. Bontcheva and Petzov [21] built a mechanical model for numerical simulation in real time closed die forging, in which the thermomechanical part of the model is successfully coupled with the microstructural evolution model. By coupling the mechanical model with a finite-element simulator, the microstructural phenomena, which has great importance for the material behavior and mechanical properties, can be taken into account in the designing of the die-forging processes. Park and co-workers developed a series of constitutive equations for dynamic recrystallization, meta-dynamic recrystallization and grain growth, and implemented them into a 3D FE simulator, enabling the evolution of grain size in the process of two-step blade forging of Alloy 718 to be simulated. Comparison of the predicted grain size with the actual microstructure of a two-step forged blade, successfully validated its effectiveness in the prediction of microstructures [22, 23]. In order to investigate the microstructure evolution of nickel-based alloy Nimonic 80A during a large exhaust valve forging, Jeong et al. [24] combined the mathematical models of microstructure evolution with a thermo-viscoplastic finite element software to predict microstructural evolution during the hot forging process. Du et al. [25] investigated microstructural evolution during the twist-compression deformation process for large-scale forging parts by coupling the microstructural evolution models with the rigid-viscoplastic FEM. In order to define the optimum forging conditions, including material temperature, strain-rate, strain, forging load and microstructural evolution, the commercial finite-element-analysis code coupled with the developed microstructural evolution modes of dynamic recrystallization was used to simulate the forging procedure of a turbine disk by Cha et al. [26], the successful outcome of this work demonstrating that general non-isothermal hot forging in air can be employed to manufacture a superalloy product.

Another important issue in hot metal forming is the prediction of microstructural evolution during multi-stage or free forging, during which DRX, SRX and MDRX are important microstructural-evolution mechanisms. Understanding the microstructural changes and softening-mechanisms taking place during the complex forming processes plays a key role in achieving the desired mechanical properties of the forgings. To date, many researches also have devoted great efforts to establishing phenomenological models to predict microstructure evolution during a complex recrystallization process. Elwazri et al. [27, 28] developed kinetics equations for SRX and MDRX for high-C microalloyed steels with V and Si additions, respectively. Dehghan-Manshadi et al. [29, 30] systematically studied the post-deformation restoration behaviour of typical austenitic stainless steel. Recently, Lin et al. [31–33] investigated SRX and MDRX behaviour in 42CrMo steel subjected to isothermally-interrupted hot-compression tests. At the same time, the kinetics equation and grain-size models of SRX and MDRX for 42CrMo steel were proposed. Chen et al. [34, 35] investigated the post-dynamic recrystallization behavior for typical heavy forging steel.

Generally, the microstructural evolution models in this approach are obtained from isothermal laboratory tests. However, there may be a temperature distribution in the workpiece due to heat transfer or plastic deformation, which could be predicted by FEM simulation coupled with the developed constitutive models. At the same time, while the approach provides information about the structure and properties that will be produced in a specific material subjected to a pre-assigned processing schedule, the calculations are required to be repeated afresh for any change in schedule or for a new material. The following are recently-reported examples of the prediction of the microstructural evolution for steels [36], magnesium alloy [37] and aluminum alloy [38] by using the phenomenological modelling method during the hot-forging process.

2.2 Prediction of the microstructural evolution in microalloyed forging steel

Microalloyed forged steels are being widely used for machinery structural parts, as they result in dramatic energy saving, by not requiring heat treatment [39]. To determine and optimize the final microstructure and mechanical properties of the hot-forged microalloyed forged steel product, using the finite-element-method (FEM), it is necessary to develop mathematical models to predict the grain size during the forging process. The microstructural evolution of microalloyed steel during the hot-forging process was investigated by Wang [36]. The dynamic recrystallized fraction was described by utilizing a modification of the Avrami equation, the parameters of which were determined by single-hit compression tests, furthermore the static recrystallization kinetic equation and grain-growth model were established using double-hit isothermal compression tests [40]. The developed models for microstructural evolution are listed in Table 3. Based on the experimental results and mathematical modelling, a three-dimensional numerical-simulation system for the prediction of microstructural evolution in multistage hot forging and in the following cooling process were developed. By utilizing the developed system, the whole multistage forging and the following cooling process of 38MnVS6(Ti) steel piston were simulated. The state of microstructural evolution in the forging and ferrite and pearlite transformation after deformation (as shown in Figure 3) were revealed in detail. The simulation results agree well with the experimental results (as shown in Figure 4), which show that the numerical simulation system can be used to design and optimize complex forging-processing techniques.

thumbnail Figure 3.

Simulation results: (a) distribution of dynamic recrystallization fraction in the workpiece after finish-forging, (b) distribution of grain size of austenite in the workpiece after finish-forging, (c) distribution of ferrite in the workpiece at different time after cooling process, (d) distribution of pearlite in the workpiece at different time after cooling [27].
thumbnail Figure 4.

Comparison of the predicted values and the experimental values of the grain size at the areas A and B.
Table 3.

Phenomenological model for different microscopic phenomena in hot working of 38MnVS6(Ti) steel.

2.3 Prediction of the microstructural evolution in magnesium alloy

Magnesium alloys are currently the lightest among structural materials, with low density, high specific strength and stiffness, superior damping capacity, high thermal conductivity, and good electromagnetic-shielding characteristics. Due to their hexagonal crystal structure, magnesium alloys have relatively low workability at room temperature but the workability is greatly increased at elevated temperature. At present, the vast majority of magnesium products are in the form of die castings. In contrast with cast magnesium alloys, wrought magnesium alloys have been widely applied in the aeronautical and astronautical, automotive and electronic industries, as a result of their fine and uniform grains and better mechanical properties. Presently, for the plastic forming processing of magnesium alloys, the studies are focused on extrusion, rolling and superplastic forming. Due to their sensitivity to temperature and strain rate, less research on the forging of magnesium alloys has been conducted. In order to investigate the complicated-shape parts forgeability of magnesium alloys, the microstructural evolution model of magnesium alloys was proposed by Liu [37]. Based on the characteristics of the dynamic recrystallization process and the feature of the limit of the exponential function, a new kinetics model of dynamic recrystallization was developed [41]:(1)where εc is the critical strain, ε0.5 is the strain for 50% DRX, and kv is a constant related to the velocity of DRX, which is mainly determined by the initial grain size and the stacking fault energy. The new kinetics model of DRX has a good ability to reflect the “slow-rapid-slow” property of DRX development. At the same time the new model has fewer parameters compared to the conventional kinetics models [11–17]. The numerical simulation of hot-forging processing by integration of the microstructural prediction model and FEM was used to evaluate the forgeability of magnesium alloy AZ31B. Based on this, a new hot-forging technique was developed and a hot-forging experiment into the forging of a spur bevel gear was carried out to validate the accuracy of the new model and method [42]. The distribution of the dynamically-recrystallized volume-fraction and grain size after finish forging is shown in Figure 5. Photographs of the spur bevel gear after the removal of the flash are shown in Figure 6. The metallographies of different areas are also shown in Figure 6. The coincidence of the predicted results with measured results validates the accuracy of the new microstructural-evolution model.

thumbnail Figure 5.

Distribution of dynamic recrystallization volume fraction (a) and grain size, (b) after finishing-forging of magnesium alloy AZ31B spur bevel gear [28].
thumbnail Figure 6.

Metalographs of the areas A, B and C in the magnesium alloy bevel gear [28].

2.4 Prediction of the microstructural evolution in wrought aluminum alloy

Wrought aluminum alloys are widely used to meet the demands of both light-weight vehicles and high-strength structural parts. Because of the high stacking fault energy of aluminum alloys, dynamic recrystallization is difficult to occur during hot deformation, which greatly differs from the hot deformation behavior of steel. Due to the large stored energy associated with severely hot deformation, static softening (static recrystallization and static recovery) and grain growth will occur during inter-pass time and cooling after deformation, which has a great impact on the final mechanical properties of the aluminum alloy products. Therefore, it is imperative for technologists and designers to investigate the static softening and grain growth behaviour of aluminum alloy during hot deformation. Recently, the material flow and microstructure evolution during multi-pass hot forging process of typical wrought aluminum alloys 6082 were systematically investigated by Li [38]. At the same time the static recrystallization kinetics model, the grain-size-evolution model and the grain-growth model were established, as shown in Table 4. Following this, the proposed microstructural models were integrated with DEFORM through developed subroutines, and then information about the kinetics of recrystallization and grain-size distribution during the multi-pass hot-forging of an automobile part were obtained by simulation. Figure 7 shows the distribution of statically-recrystallized volume-fraction and average grain-size for a holding time of 380 s after the final-forging process were determined by the proposed muti-physics coupling simulation system. Figure 8 gives the optical microstructure of the final product at different metallographic examination areas. From the figure, it can be found that the recrystallization is complete, and that the grain growth which occurs agrees well with the numerical-simulation results. Additionally, the figure also indicates that the developed muti-physics coupling simulation system is suitable for the numerical simulation of the hot-forging process of complex-shaped parts of 6082 aluminum alloy, and can provide theoretical guidance for process design and improvement during an industry manufacturing process. Furthermore, the modelling and simulation method can be extended to other wrought aluminum alloys.

thumbnail Figure 7.

Distribution of static recrystallized volume fraction (a) and average grain size, (b) during holding period after final-forging [29].
thumbnail Figure 8.

Metallography of the posterosuperior control arm of Zones A and B [29].
Table 4.

Phenomenological model for different microscopic phenomena in hot working of 6082 aluminum alloy.

3 Physically-based on internal variable model

The material constants of the macro phenomenological models can be obtained through fitting and regressing experimental data. Phenomenological models are easier to be combined with commercial FE software. However, it is obvious that there are some potential deficiencies in phenomenological models, therefore, experimental results cannot be well described, especially when under relatively high-strain-rate and temperature conditions. During a hot and dynamic deformation process, the internal microstructure of the material changes extensively, therefore phenomenological models are not able to give an accurate interpretation. Large errors will occur when models are used beyond their designed experimental applicability: then it seems to be necessary to use a method based on a physical mechanism to establish microstructural evolution models which consider the mechanism of deformation such as dislocation dynamics, thermal activation and so on. Recently, many physically-based models have been proposed [37–48].

The microstructural evolution may be described by many different internal state variables, the most relevant to choose depending on the problem: many important problems are well characterized by two or only one variable. At the highest microstructural level, grain size is a common parameter, or the volume fraction of grains of different types, or the fraction of solid in solidification. Below this level are characteristics of deformation substructures, i.e., subgrain size, dislocation density, or sub-boundary mis-orientation, second-phase particles. Roters et al. [44] developed a new microstructural strain-hardening model of polycrystals by introducing three internal state variables (3IVM): mobile dislocations, immobile dislocations in the cell interiors and immobile dislocations in the cell walls. By comparison of the behavior of a two-phase commercial alloy with a precipitate-free model alloy, it was shown that the 3IVM is capable of adequately predicting the stress-strain curves of two-phase aluminum alloys at elevated temperatures. Lin et al. [45] developed a set of unified viscoplastic constitutive equations for a micro-alloyed steel based on dislocation theory by using the recrystallized fraction as the internal state variable. Estrin [46] developed a physical model for superalloys which simulates microstructural evolution during the hot-working process of nickel and uses the dislocation density as an internal state variable. Steinmetz et al. [47] developed a new physics-based constitutive model for low-SFE fcc metals based on a combination and extension of the 3IVM [44] and the twin-nucleation model by using dislocation cells, grain size and twin volume-fraction as the internal state variables.

Jin [48] developed a thermal viscoplastic constitutive model considering dynamic recrystallization. Jin’s model is characterized by the physical variables in the recrystallized zone and in the un-recrystallized zone being treated, respectively, according to the basic microscopic mechanism [49]. The model developed by Jin has the ability to predict the duplex-grain defect in which it applies the average grain-size and the maximum grain-size difference to describe the final grain-size distribution. Qu et al. [50] made some local improvements on Jin’s model in order to perfect the model in theory and to allow it to work more smoothly in the numerical simulation software. Qu et al. [51] also enriched the method of identification of the material parameters by inverse analysis for an improved viscoplastic model considering dynamic recrystallization.

Sun et al. [52] proposed an internal state variable model for microstructural evolution of TA15 alloy including the dislocation-density rate equation, the recrystallization-fraction rate equation and the grain-growth rate equation, as in the following equations:(2)where k1, k2, k3, k4, α1, α2, γ1, γ2, γ3, β1, β2, λ1, m, n, q, Qs and Qb are material constants to be determined from experimental data. By integrating the microstructural-evolution model within the DEFORM-3D software package, the microstructural evolution during hot compression deformation and isothermal forging of a large component was predicted. The agreement between the experimental results and the simulation indicates that the developed model based on internal state variable theory is reliable and practical.

Fan et al. [53] established a theoretical model which considers the fundamental metallurgical principles of dynamic recrystallization and uses the mobile grain-boundary area, the immobile grain-boundary area and the dislocation density as the internal state variables. An internal-state-variable based self-consistent constitutive model was proposed for unified prediction of the flow stress and the microstructural evolution during the hot-working of wrought two-phase titanium alloys in both the single-beta region and the two-phase region [54].

Further, with the rapid development of micro-electro-mechanical systems and micro-system technology, the microstructure, such as grain size, orientation and dislocation density, shows a more evident effect on the mechanical behaviour of metallic polycrystalline material as the length-scale decreases. Dislocation-density based crystal plasticity models combined with the finite-element method (CPFE) have been shown to be useful for investigating the micromechanical behavior and microstructural evolution of materials, especially for the current trend towards device miniaturization. Various efforts have been devoted to develop physically-based crystal plasticity theories [55].

As noted in the above review, with the development of microstructural modelling and the definition of metal-forming mechanisms, the internal-state-variable model has been greatly developed over the past two decades. The state variable formalism has been used to describe non-isothermal transformation behaviour in a variety of systems ranging from steels and cast iron to aluminum alloys and titanium alloys. It is particularly well-suited to the development of models for non-isothermal transformation behaviour. Generally, the internal-state variable has the ability to describe the interaction between deformation and microstructure. However, it can also be found that this model has numerous variables and parameter values which are hard to determine, as well as a low calculation efficiency. Therefore, in recent years, research on the internal-state-variable approach has been mainly focussed on parameters identification [56–59].

4 Mesoscale model

Over the past two decades, with the rapid development of computer technology and a thorough understanding of microstructural evolution thermodynamics and kinetics, mesoscale methods have been successfully used to simulate microstructural evolution in hot metal forming. At this scale, the evolution of the microstructure is represented by some basic microstructural constituents such as the grain orientation. This means that the actual microstructures can be predicted at mesoscale and the statistical information of internal variables used in the macro-scale models are just the inevitable results. For instance, the following mainly introduces the mesoscale CA model used in the prediction of microstructural evolution during hot forging.

4.1 Formal description of CA

Cellular automata (CA) are synchronous algorithms that describe the discrete spatial and temporal evolution of complex systems by applying local deterministic or probabilistic transformation rules to lattice cells with local connectivity [67]. In 2D and 3D CA representations of microstructure, interfaces between neighbouring grains are lines and surfaces and need to be approximated within the CA grid. The most classic form is a periodic grid of squares or cubes. Other types of grids are possible, as illustrated in Figure 9. Classic grids of cells come with classic definitions of the neighbourhood, and the most known are definitely the von Neumann, Moore and extended Moore neighbourhood definitions on a 2D square grid of cells, as illustrated in Figure 10. In these types of neighbourhood, of which a multitude of shapes can be imagined, a cell (the cell shown in red in the figure) is part of its own neighbourhood, which is the usual case when using cellular automata in microstructural evolution modelling.

thumbnail Figure 9.

Types of periodical cellular automaton grids in two and three dimensions.
thumbnail Figure 10.

Classic neighborhood definitions.

4.2 CA model for normal grain growth

Grain growth is one of the most important mechanisms in the control of microstructural evolution during the hot-forging process [68]. The energy of grain boundaries at equilibrium and topological requirements are considered as two important factors in the modelling of grain growth. From a more general point of view, normal grain growth is one of the natural structural evolving processes, during which the grain boundary network is similar to the pattern of biological cells, geographical and ecological territories, and they have some similar characteristics. Beck et al. [69] pointed that all grains grow at roughly the same rate during the process of normal grain growth. The grain growth kinetic equation has also been established by Beck et al. [70]. Experimental results suggest that the grain-size distribution is approximately log-normal for normal grain growth [71, 72].

Liu et al. [68] proposed a CA model for the simulation of normal grain growth, which can flexibly and fully represent normal grain growth with the virtue of linking topological requirements and energy requirements together and give the correct distribution of the sides, the size distribution, growth kinetics and microstructural evolution. However, Liu did not consider the probabilistic jumping of atoms in boundaries and boundary movement in the CA models. Geiger et al. [73] developed a CA simulation model to investigate the effects of maximum orientation number, temperature and activation energy on grain growth kinetic by considering the atoms jumping in grain boundaries. Recently, by introducing the effect of the basic physical metallurgical principles, such as the thermodynamic driving mechanism, the curvature-driven mechanism and the lowest energy principle, into CA models, Raghavan et al. [74, 75], He et al [76] and Chen et al. [77] quantitatively simulated topological and kinetic features during normal grain growth. However, the influence of boundary anisotropy and second-phase particles on grain growth were ignored in these CA models so that there was a difference between CA simulation results and experimental observations. Considering the effect of solute drag and anisotropic mobility of grain boundaries, Wu et al. [78] developed a CA model to predict the grain coarsening of titanium alloys.

Figure 11 shows two-dimensional and three-dimensional CA simulation results for normal grain growth. Figure 12 shows the evolution of the grains with different sides in the process of normal grain growth by CA simulation. As shown in the figure, this implies that the grains with more than six sides will grow and grains with less than six sides will shrink, while the grains with sides equal to six will neither grow nor shrink. This tendency accords with the energy-decrease principle and the normal grain-growth theory [76].

thumbnail Figure 11.

CA simulation of the normal grain growth (a) two-dimensional CA simulation, (b) three-dimensional CA simulation.
thumbnail Figure 12.

Illustration of different sided grains (a) a four-sided grain, (b) a five-sided grain, (c) a six-sided grain.

Generally, by introducing the principles of physical metallurgy, such as the curvature-driven mechanism, thermodynamic driving mechanism and the lowest energy principle, the CA model has the ability to predict normal grain growth during the heating process for metals and alloys before deformation during hot forging. It also confirms the input data for the following CA simulation for recrystallization.

4.3 CA model for recrystallization

Recrystallization usually refers to a process composed of the formation and grain growth of new recrystallized grains. Grain boundaries and deformed bands are preferable to nucleation sites to initiate nuclei due to their sufficient energy, which is followed by nuclei growth driven by thermodynamic energy, boundary energy or stored deformation energy. When the process takes place during the forming stage it is called dynamic recrystallization, otherwise it is called static recrystallization. Obviously, the only difference between them is that the process of nucleation and growth of newly unstrained nuclei occurs during the deformation process for the former while the same process takes place after deformation for the latter [79].

4.3.1 Modelling of dislocation evolution

During plastic deformation, dislocations are created by work hardening and annihilated by dynamic recovery. To describe the deformation behavior of austenite, the Kocks-Mecking model [80] is employed, in which the flow stress is proportional to the square root of dislocation density as given in:(3)where α is a dislocation-interaction term which is around 0.5 for most metals, b is Burger’s vector, μ is the shear modulus and ρmean is the mean dislocation density. In CA simulation ρmean can be expressed as:(4)where Ntotal is the total number of cells in the CA model and ρi·j is the dislocation density of site (i, j). The dislocation hardening and recovery are modeled by the change in the dislocation density exactly as proposed by Estrin [81]. The variation of the dislocation density of site (i, j) with respect to strain can be expressed as [82]:(5)where the two terms represent a competition between storage of mobile dislocations and dynamic annihilation of dislocations, k1 represents work hardening, k2 is the softening parameter that represents the recovery of dislocations. k1 and k2 in equation (5) can be evaluated from the measured flow stress, and can be expressed as functions of temperature and strain rate.

By integrating equation (5), the following expression is obtained:(6)where ρ0 is calculated using equation (3), and σ0 is obtained from the flow stress.

Once , it can be determined that:(7)where ρsaturation is the saturation dislocation density. Substituting equation (7) into equation (6) gives:(8)where σWH is the flow stress in the work-hardening stage. For a certain deformation condition, substituting σWH, σ0 and σsaturation into equation (8) gives the value of k2. From equation (7), the value of k1 can be obtained as:(9)

A recovery process takes place following hot-deformation in engineering alloys at a quite high temperature, where the edge dislocation climb can be assumed to be the main recovery mechanism. When deformation is interrupted, the actual dislocation density inside each cell is calculated from its current dislocation density.

Marx et al. [83] employed the following equation to describe the dislocation density evolution:(10)where is the dislocation density inside each cell when deformation is interrupted. The time-constant τ can be expressed in terms of Boltzman’s law and contains the temperature dependency.

Kugler and Turk [84] adopted a similar exponential equation to calculate the dislocation density, as shown below:(11)

When deformation is interrupted, during each time step (Δt) the new dislocation density inside each cell is calculated from its current dislocation density ().

4.3.2 Modelling of nucleation and grain growth

The onset of nucleation of DRX is usually associated with the accumulation of dislocations. When the dislocation density of a deforming matrix reaches a critical value (ρcritical) during thermomechanical processing, nucleation of DRX will be initiated. ρcritical is calculated using equation (3). Nucleation of DRX is handled by randomly choosing a certain fraction of the total cells located on grain boundaries (including primary grain boundaries and R-grain boundaries) as the new nucleus at each CA simulation step. Each nucleus consists of one cell. The orientations of the nucleus are randomly set in the program, and are represented by random integer in the range 1–180. When such a nucleus is placed in the system, it is initially assigned a stored energy of zero, that is ρi,j, and increases with increasing strain based on equation (5). The nucleation rate per unit grain boundary area for DRX can be expressed as [82]:(12)where Cdynamic is a constant, m is set to 1.0 in the present simulation, Qact is the activation energy, is the strain rate, R is the universal gas constant (8.31 Jmol−1 K−1) and T is the absolute temperature. There are two basic methods to calculate the constant (Cdynamic). First, the percentage of DRX (η) can be experimentally measured for a specific deformation condition [82], then the constant Cdynamic in equation (12) can be determined for a deforming material. Second, the constant Cdynamic can be determined using an inverse analysis method [85, 86]. The dislocation density of R-grain evolves from zero to a saturated value. The difference between the dislocation densities of R-grain and the matrix supplies the thermodynamic driving force for the growth of R-grain. It is generally assumed that the velocity of grain boundary movement fulfills the following equation [87]:(13)where M is the grain boundary mobility, which can be calculated by the following equation [82]:(14)where δ is the characteristic grain boundary thickness, Dob is the boundary self-diffusion coefficient, Qb is the grain boundary diffusion activation energy, K is the Boltzmann’s constant.

It is assumed that the R-grain is spherical. The driving force Δf can be expressed as: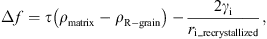(15)where ρmatrix is the dislocation density of the matrix, ρR-grain is the dislocation density of the ith R-grain, τ is the dislocation line energy (τ = cμb2) (c is a constant equal to 0.5). The 2D simulation metallography is viewed as a cross-section of the corresponding 3D microstrcuture. Following [88, 89], an equivalent average radius of a grain is used to define the recrystallized grain size, and is calculated by using the following equation:(16)where Ni is the total number of cells belonging to the recrystallized grain and where Acell is the area of one cell.

The grain boundary energy (γi) can be calculated by the Read-Shockly equation:(17)where θi is the misorientation between the ith R-grain and its neighbouring grain. The grain boundary energy of high angle boundary can be directly calculated as follows [90]:(18)where γm, θm are the boundary energy and the misorientation when the grain boundary becomes a high angle boundary (taken as 15°), respectively. ν is Poisson’s ratio. During continued deformation, the dislocation density of the R-grains, as well as the primary grains, changes with the strain following the rule of equation (5). In the CA simulation, the time step (Δt) is defined as the ratio between the cell diameter (d0) and maximum grain boundary velocity (νmax). Similar to the treatment reported by Kugler and Turk [84], it can be calculated by:(19)

Then the strain increment (Δε) is dependent on strain rate as . The increase in the distance of the grain boundary at time t can be calculated as:(20)

The occurrence of static recrystallization is usually described as taking place in two stages: nucleation and growth of new grains. The process of nucleation is thermally activated and requires an incubation time before the nuclei become detectable. Ivasishin et al. [91] calculated the nucleation rate by the following equation:(21)where Cstatic is a constant, VΩ (t) is the fraction of volume at which nucleation is still possible at time t, H is the stored energy of deformation and Hmin is the minimum stored energy to cause nucleation. As for steel, the critical strain for the initiation of SRX is above 10 pct. The deformation stored energy can be calculated according to the dislocation density:(22)where C0 is a constant with a value in the range of 0.5–1, Vr is the molar volume of austenite and ρ is the dislocation density inside each cell. For the other issues, there is no distinction between the dynamic and static processes. Thus equations (13)–(20) are used to describe the growth of new grains.

Once dynamic recrystallization is initiated during deformation, the dynamically recrystallized nuclei continue to grow after deformation is interrupted. This mechanism was identified by Petkovic et al. [92] as metadynamic recrystallization. Unlike static recrystallization, metadynamic recrystallization apparently does not require incubation time, because it makes use of the nuclei formed during dynamic recrystallization. Thus the same governing equations (13)–(20) are used to describe the growth of new grains.

4.3.3 Implementation of recrystallization in the CA model

Generally speaking, the CA framework for recrystallization has the similar form which is composed of the following parts [79, 93]:

  1. Generation of initial microstructure for nucleation and grain growth;

  2. Definition of the cell neighbourhood;

  3. Assignment of state variables to each cell;

  4. Definition of switching rules for CA models.

Generally, the initial microstructure before recrystallization is created by running a CA program of normal grain growth, as description in Section 4.2. Usually, according to the von Neumann or Moore neighbourhood, there are four or eight neighbours to each cell. Some state variables, such as random orientation number, initial dislocation density or grain boundary and so on, are assigned to each cell. Based on the state value of each cell, a switching rule that well corresponds to the physical process is specified. Finally, the CA simulation of microstructural evolution is realized by interaction of middle and neighbouring cells variables of each cell which are updated.

In recent years, m any researchers have successfully described recrystallized nucleation and grain growth using the CA method. In their work, Goetz et al. [94], Raabe et al. [67], Ding et al. [82] and Kugler and Turk [84] contributed greatly to the development of the CA method for the simulation of recrystallization. Recently, based on Ding et al. [82] and Kugler and Turk [84] work, Yazdipour et al. [95] simulated DRX during thermomechanical deformation in 304 austenitic stainless steel by the CA method. In this case, initial grain size, initial grain orientation and dislocation density were used as input data to the CA model, and flow curve, dislocation density, finial grain size and orientation, and DRX volume fraction were the output data. Hållberg et al. [88] employed a cellular automaton algorithm with probabilistic cell switches in the simulation of dynamic discontinuous recrystallization in pure Cu. Ding et al. [96] investigated the hot compression behaviour of the Mg-9Al-1Zn alloy using EBSP analysis and the CA method.

Chen et al. [90] predicted the DRX in an ultra-super-critical rotor steel. As shown in Figure 13, by using the CA method, the microstructural evolution of the steel with the changing of the strain was illustrated. The regions in different colours represent the newly formed recrystallized grains with different crystallographic orientations and the white regions correspond to the deformed matrix. It is noted that the new nuclei for DRX form on grain boundaries when the strain reaches about 0.25. With increasing the strain, the recrystallized grains grow after nucleation, at the same time the nucleation of new recrystallized grains takes place.

thumbnail Figure 13.

Predicted microstructural evolution of 30Cr2Ni4MoV rotor steel at the temperature of 970 °C and strain rate of 0.1 s−1 with the CA model. The strains are: (a) 0.25, (b) 0.35, (c) 0.45 and (d) 0.5, respectively [83].

The deformation of grain shape makes a change in grain boundary and consequently affects nucleation and growth of nuclei during recrystallization. To describe the effect of compression on the grain shape more accurately, an updated CA model was proposed in which a cellular coordinate system and a material coordinate system were established separately [93, 97, 98]. When the topological-deformation technique is used, the result obtained using the developed CA model is closer to the experimental results [93], as shown in Figure 14.

thumbnail Figure 14.

The CA model coupling the topology technology [79, 83, 84].

The austenite grain evolution during multi-pass deformation of 30Cr2Ni4MoV steel was simulated using the developed CA model, during which DRX, SRX and MDRX take place. The predicted grain sizes were compared with measured ones of the steel in Figure 15. It can be seen that the prediction agree satisfactorily with the experimental results. This also indicates that the developed CA model can be used to predict the microstructural evolution during a complex hot-forging process. By coupling the FEM method and the CA method, numerical simulations for a multi-stroke and multi-pass stretching process were performed, as shown in Figure 16. This provides a novel way for investigating the microstructural evolution during the complicated recrystallization processes observed in heavy forging production on a multi-scale.

thumbnail Figure 15.

Comparison of the simulated, average grain-sizes after each pass, with the experimental results [79, 83].
thumbnail Figure 16.

Comparison of two simulations: (a) distribution of macroscopic quantities from the FEM simulation, and (b) mesoscale simulation results after four-pass stretching by CA simulation [83].

4.4 CA model for phase transformations

It is well known that the mechanical properties of hot-forged steels are strongly influenced by the grain size and the volume fraction of the matrix phase. Therefore, modelling of phase transformation from hot-deformed austenite to ferrite, pearlite and bainite is a powerful method to control the microstructure of steels and improve their mechanical properties. This topic has become one of the most important research fields in the physical metallurgy of steels in recent years [99]. However, because the effects of hot deformation on phase transformation behavior are very complex, mathematical models of phase transformation from work-hardened austenite were usually established by regression with experimental data. These regression models are not accurate enough and can only be used over a small range, which latter depends on the experimental data. Recently, Zheng et al. developed an integrated CA model to simulate dynamic strain-induced transformation (DSIT) in low-carbon steels [100, 101]. Following that, a modified CA model was developed to simulate the microstructural evolution during post-dynamic transformation (post-DT) after DSIT. The CA model for phase transformation developed by Zheng and Raabe provides a novel way for investigating the microstructural evolution during post-DT [102, 103].

5 Artificial neural network (ANN) model

Generally, the prediction of the microstructural evolution for metals and alloys during a hot-forging process is usually described by the above-reviewed phenomenological, physical-based or mesoscale models. The responses of the deformation behaviour of the materials under elevated temperatures and strain rates is highly non-linear, and many factors affecting the microstructure evolution are also non-linear, which make the accuracy of grain-size prediction by regression methods low and the pplicable range limited. However, the field of neural networks can be thought of as being related to artificial intelligence, machine learning, parallel processing, statics, and other fields. The attraction of artificial neural networks (ANN) is that they are best suited to solve the problems that are the most difficult to solve by traditional computational methods. ANN can provide a fundamentally different approach to materials modelling and material-processing control techniques than statistical or numerical methods. One of the main advantages of this approach is that it is not necessary to postulate a mathematical model at first or identify its parameters using a neural network. In recent years, some efforts have been made on the applications of ANN in industry or academic study [108–114].

ANN are a large class of parallel processing architectures, which can mimic complex and non-linear relationships through the application of many non-linear processing units called neurons. The relationship can be “learned” by a neural network through adequate training from the experimental data. It can not only make decisions based on incomplete and disorderly information, but can also generalize rules from those cases on which it was trained and apply these rules to new cases. Usually, the structure of an ANN is hierarchical with neurons grouped in different layers designed as an input layer, hidden layers and on output layer, as shown in Figure 17. Signals are supplied to the neurons of the input layer; each neuron of this layer then generating an output signal, which is transferred to the neurons of the hidden layer. The output signals are generated by the last layer (output layer). Of course, there is no theoretical limit on the number of hidden layers but typically there are just one or two. A maximum of four layers (three hidden layers plus an output layer) are enough to solve problems of any complexity. The multi-layer feed-forward network with back propagation (BP) learning is the most popular of all ANN models. The feed-forward back-propagation neural network is actually composed of two neural network algorithms: (a) feed forward and (b) back propagation. It is not necessary to always use “feed forward” and “back propagation” together, but this is usually the case [109].

thumbnail Figure 17.

Schematic structure of a back propagation neural network.

The convergence criterion for the network is determined by the average root-mean-square (RMS) error between the desired and predicted output values, given as:(23)where ERMS is the average RMS, N is the number of training or testing data, p is the number of variables in the output, dj(n) and yj(n) are the target output and network output for neuron j, respectively. For the prediction of the grain size of the hot deformed material, strain, strain rate and temperature are often used as the inputs of the model, while the grain size is the output of the ANN model. At the same time, ANN requires that the range of both input data and output data should be 0–1, consequently the data must be unified.

Li et al. [110, 111] developed a model for microstructural evolution of the TC6 alloy, including the grain size and volume fraction of the α phase, by coupling an ANN and a fuzzy set (FNN), then the numerical simulation of microstructural evolution during forging was proposed by combining the ANN model with the FE simulation results. Recently, Li et al. [112] established an ANN model for microstructural evolution of the TC11 alloy during isothermal forging. The predicted grain size and volume fraction are in good agreement with the experimental results. Kim et al. [113] investigated the microstructural evolution of titanium alloy under isothermal and non-isothermal hot-forging conditions by using ANN and FE simulation. An essential feature of Kim’s work is that the ANN codes consist of two parts: the first part is for the phase volume-fraction change under isothermal conditions and the second part is for the non-steady state. By comparison between the experimental data and the calculated alpha-phase volume-fraction presented by the ANN model, a very good correlation between experimental and predicted result has been obtained, which indicates the excellent capability of the developed ANN model to predict the volume fraction, grain size and dynamic globularization ratio of alpha phase. Sun et al. [114] developed a computer code written in FORTRAN to exploit an improved BP neural network model, and the code has been embedded in the software DEFORM. Isothermal extrusion of the TA15 alloy has been simulated and the grain-size predicted. Comparison between the simulated grain-size at different pressing speeds during the isothermal extrusion of the TA15 alloy and the predictions, indicates that the model has a high prediction precision.

6 Summary and perspective

Microstructural evolution of metals and alloys largely affects the mechanical and functional properties of final products. Numerical modelling for this process has become a currently active topic both in industrial and scientific fields. In this paper, the principal methods for modelling the phenomenon of microstructural evolution during the hot-forging process have been reviewed. According to their mechanism and characteristics, these models are divided into four categories: phenomenological, physical-based, mesoscale and artificial neural network models. For each kind of these models, some typical examples were given and discussed in this paper. However, not all models are included, due to the length limitations of this review article. Some important conclusions can be made as follows:

  1. The particular characteristics of phenomenological models is that it is not necessary to gain a detailed understanding of the physical phenomena involved in the deformation process. The material constants associated with these models are usually obtained by the regression analysis. It is easy to integrate these models into the commercial software to predict microstructure evolution during hot forging. The future of the modelling method lies most likely in obtaining more accurate model parameters over a wide range of process conditions based on the hot-forging scheme.

  2. The particular advantage of physically-based models is that these models take into account the thermal deformation mechanism of metals and alloys in the hot-deformation process, which includes work-hardening due to dislocation and dislocation interactions, and dynamic softening ascribed to thermal activation. There are many material parameters in the physically-based microstructural-evolution models. The major drawback of physically-based model is the determination of the material parameters. Usually, the determination of these material parameters requires some precision items of apparatus. Therefore, in recent years the research on physically-based modelling has mainly been focussed on parameter identification.

  3. The mesoscale CA approach provides a powerful tool for quantitative and explicit simulation of microstructural evolution during hot metal-forming processes. By tracking the evolution of the dislocation density, CA coupling FEM could be developed as a means of predicting the microstructural evolution during hot forging. Nevertheless, the application of the present mesoscopic CA model is limited by some empirical features. For instance, the nucleation parameters and selection of nucleation sites have to be determined by the experiment fitting or artificial setting due to the absence of physical criteria or models. Therefore, it is highly necessary to develop new method to accurately determine the physical constants used in CA simulation through theoretical and experimental means or by use of some other analysis methods.

  4. The main advantage of ANN models in this context is their versatility to solve the problems that are the most difficult to solve by traditional computational methods. However, the successful application of an ANN model is strongly dependent on the availability of extensive, (delete the) high-quality data and characteristic variables, as the modelling offers no physical insight.

Acknowledgments

The authors gratefully acknowledge the financial support from the National Science and Technology Major Project of China (Grant No. 2012ZX04012011), National Basic Research Program of China (Gran No. 2011CB012903), China Postdoctoral Science Foundation (Grant No. 2013M531171) and Shanghai Jiaotong University Postdoctoral Science Foundation.

References

  1. W. Roberts, The metallurgical Society of AIME 56 (1982) 109. [Google Scholar]
  2. B.Y. Xu et al., Int. J. Mech. Sci. 48 (2006) 190. [CrossRef] [Google Scholar]
  3. F. Chen et al., Mater. Sci. Eng. A 528 (2011) 5073. [CrossRef] [Google Scholar]
  4. T.M. Pollock et al., J. Propuls. Power 22 (2006) 361. [Google Scholar]
  5. C.M. Sellars, Mater. Sci. Technol. 6 (1990) 1072. [CrossRef] [Google Scholar]
  6. H.J. McQueen, Mater. Sci. Eng. A 387–389 (2004) 203. [Google Scholar]
  7. C.M. Sellars et al., Metal Sci. 13 (1979) 187. [CrossRef] [Google Scholar]
  8. V.V. Kutumbarao et al., Bull. Mater. Sci. 19 (1996) 677. [CrossRef] [Google Scholar]
  9. H.J. McQueen et al., J. Mater. Process. Technol. 53 (1995) 293. [CrossRef] [Google Scholar]
  10. H. Yada et al., JSTP 27 (1986) 33. [Google Scholar]
  11. R. Kopp et al., Advanced Technology of Plasticity 24–28 (1987) 1229. [Google Scholar]
  12. A. Laasraoui et al., Metall. Trans. A 22 (1991) 151. [CrossRef] [Google Scholar]
  13. S. Nanba et al., ISIJ Int. 32 (1992) 377. [CrossRef] [Google Scholar]
  14. P.D. Hodgson et al., ISIJ Int. 32 (1992) 1329. [CrossRef] [Google Scholar]
  15. S.-I. Kim et al., Mater. Sci. Eng. A 311 (2001) 108. [CrossRef] [Google Scholar]
  16. S.-I. Kim et al., Mater. Sci. Eng. A 355 (2003) 384. [CrossRef] [Google Scholar]
  17. S. Serajzadeh et al., Mech. Res. Commun. 30 (2003) 87. [CrossRef] [Google Scholar]
  18. J. Liu et al., Mater. Sci. Eng. A 529 (2011) 300. [CrossRef] [Google Scholar]
  19. A. Dehghan-Manshadia et al., Mater. Sci. Eng. A 485 (2008) 664. [CrossRef] [Google Scholar]
  20. Y.-S. Jang et al., J. Mater. Process. Technol. 101 (2000) 85. [CrossRef] [Google Scholar]
  21. N. Bontcheva et al., Comput. Mater. Sci. 28 (2003) 563. [CrossRef] [Google Scholar]
  22. N.K. Park et al., J. Mater. Process. Technol. 111 (2001) 98. [CrossRef] [Google Scholar]
  23. Y.-S. Na et al., J. Mater. Process. Technol. 141 (2003) 337. [CrossRef] [Google Scholar]
  24. H.S. Jeong et al., J. Mater. Process. Technol. 162–163 (2005) 504. [CrossRef] [Google Scholar]
  25. F.S. Du et al., J. Mater. Process. Technol. 187–188 (2007) 591. [Google Scholar]
  26. D.-J. Cha et al., Int. J. Precis. Eng. Manuf. 12 (2011) 331. [CrossRef] [Google Scholar]
  27. A.M. Elwazri et al., ISIJ Int. 44 (2004) 162. [CrossRef] [Google Scholar]
  28. A.M. Elwazri et al., ISIJ Int. 44 (2004) 744. [CrossRef] [Google Scholar]
  29. A. Dehghan-Manshadi et al., Metall. Mater. Trans. A 39 (2008) 1359. [CrossRef] [Google Scholar]
  30. A. Dehghan-Manshadi et al., Metall. Mater. Trans. A 39 (2008) 1371. [CrossRef] [Google Scholar]
  31. Y.C. Lin et al., Mater. Sci. Eng. A 501 (2009) 229. [CrossRef] [Google Scholar]
  32. Y.C. Lin et al., J. Mater. Process. Technol. 209 (2009) 2477. [CrossRef] [Google Scholar]
  33. Y.C. Lin et al., J. Mater. Sci. 44 (2009) 835. [CrossRef] [Google Scholar]
  34. F. Chen et al., Mater. Sci. Eng. A 540 (2012) 46. [CrossRef] [Google Scholar]
  35. F. Chen et al., J. Mater. Eng. Perform. (2014), DOI: 10.1007/s11665-014-1083-8. [Google Scholar]
  36. J. Wang, PhD thesis, Shanghai Jiaotong University, 2007. [Google Scholar]
  37. J. Liu, PhD thesis, Shanghai Jiaotong University, 2008. [Google Scholar]
  38. X.S. Li, PhD thesis, Shanghai Jiaotong University, 2010. [Google Scholar]
  39. D.J. Naylor, Mater. Sci. Forum 284–286 (1998) 83. [CrossRef] [Google Scholar]
  40. J. Wang et al., Acta Metall. Sin. 19 (2006) 279. [CrossRef] [Google Scholar]
  41. J. Liu et al., Mater. Sci. Eng. A 529 (2011) 300. [CrossRef] [Google Scholar]
  42. J. Liu et al., J. Mater. Process. Technol. 209 (2009) 5871. [CrossRef] [Google Scholar]
  43. E.P. Busso et al., Int. J. Plast. 14 (1998) 319. [CrossRef] [Google Scholar]
  44. F. Roters et al., Acta Mater. 48 (2000) 4181. [CrossRef] [Google Scholar]
  45. J. Lin et al., J. Mater. Process. Technol. 143–144 (2003) 281. [CrossRef] [Google Scholar]
  46. Y. Estrin, Mater. Sci. Eng. A 463 (2007) 171. [CrossRef] [Google Scholar]
  47. D.R. Steinmetz et al., Acta Mater. 61 (2013) 494. [CrossRef] [Google Scholar]
  48. Q.L. Jin, J. Plastic Eng. 1 (1994) 3. [Google Scholar]
  49. B.Y. Xu et al., Int. J. Mech. Sci. 48 (2006) 190. [CrossRef] [Google Scholar]
  50. J. Qu et al., Acta Mech. Sin. 20 (2004) 499. [CrossRef] [Google Scholar]
  51. J. Qu et al., Int. J. Plast. 21 (2005) 1267. [CrossRef] [Google Scholar]
  52. Z.C. Sun et al., Mater. Sci. Eng. A 527 (2010) 3464. [CrossRef] [Google Scholar]
  53. X.G. Fan et al., Mater. Sci. Eng. A 527 (2010) 5368. [CrossRef] [Google Scholar]
  54. X.G. Fan et al., Int. J. Plast. 27 (2011) 1833. [CrossRef] [Google Scholar]
  55. F. Roters et al., Acta Mater. 58 (2010) 1152. [CrossRef] [Google Scholar]
  56. J.P. Ponthot et al., Comp. Meth. Appl. Mech. Eng. 195 (2006) 5472. [CrossRef] [Google Scholar]
  57. A. Andrade-Campos et al., Int. J. Plast. 23 (2007) 1349. [CrossRef] [Google Scholar]
  58. J. Qu et al., J. Mater. Process. Technol. 197 (2008) 212. [CrossRef] [Google Scholar]
  59. K. Spranghers et al., Int. J. Solids Struct. 51 (2014) 210. [CrossRef] [Google Scholar]
  60. D. Raabe et al., Continuum scale simulation of engineering materials, Wiley, Weinheim, 2004. [CrossRef] [Google Scholar]
  61. K.G.F. Janssens et al., Computational materials engineering – an introduction to microstructure evolution, Academic Press, Elsevier, 2007. [Google Scholar]
  62. N.M. Xiao et al., Sci. China Tech. Sci. 55 (2012) 341. [CrossRef] [Google Scholar]
  63. D. Raabe, Annu. Rev. Mater. Res. 32 (2002) 53. [CrossRef] [Google Scholar]
  64. D. Raabe et al., Model. Simul. Mater. Sci. Eng. 8 (2000) 445. [CrossRef] [Google Scholar]
  65. D. Raabe et al., Comput. Mater. Sci. 34 (2005) 299. [CrossRef] [Google Scholar]
  66. X.Y. Song et al., Acta Mater. 54 (2006) 5541. [CrossRef] [Google Scholar]
  67. D. Raabe et al., Philos. Mag. 79 (1999) 2339. [CrossRef] [Google Scholar]
  68. Y. Liu et al., Scripta Mater. 34 (1996) 1679. [CrossRef] [Google Scholar]
  69. P.A. Beck et al., J. Appl. Phys. 21150 (1950). [Google Scholar]
  70. P.A. Beck et al., Phys. Rev. 71 (1947) 555. [CrossRef] [Google Scholar]
  71. K.G.F. Janssens, Math. Comput. Simulat. 80 (2010) 1361. [Google Scholar]
  72. B.-N. Kim et al., Mater. Trans. JIM 44 (2003) 2239. [CrossRef] [Google Scholar]
  73. J. Geiger et al., Acta Mater. 49 (2001) 623. [CrossRef] [Google Scholar]
  74. S. Raghavan et al., Mater. Sci. Eng. A 445–446 (2007) 203. [CrossRef] [Google Scholar]
  75. S. Raghavan et al., Comput. Mater. Sci. 46 (2009) 92. [CrossRef] [Google Scholar]
  76. Y.Z. He et al., Mater. Sci. Eng. A 429 (2006) 236. [CrossRef] [Google Scholar]
  77. F. Chen et al., Mater. Sci. Eng. A 527 (2010) 5539. [CrossRef] [Google Scholar]
  78. C. Wu et al., Chin. Sci. Bull. 57 (2012) 1473. [CrossRef] [Google Scholar]
  79. H. Yang et al., Science China 54 (2011) 2107. [CrossRef] [Google Scholar]
  80. H. Mecking et al., Acta Metall. 29 (1981) 1865. [CrossRef] [Google Scholar]
  81. Y. Estrin et al., Acta Metall. 32 (1984) 57. [CrossRef] [Google Scholar]
  82. R. Ding et al., Acta Mater. 49 (2001) 3163. [CrossRef] [Google Scholar]
  83. V. Marx et al., Acta Mater. 47 (1999) 1219. [CrossRef] [Google Scholar]
  84. G. Kugler et al., Acta Mater. 52 (2004) 4659. [CrossRef] [Google Scholar]
  85. Z.Y. Jin et al., Mater. Sci. Eng. A 527 (2010) 3111. [CrossRef] [Google Scholar]
  86. Z.Y. Jin et al., Comput. Mater. Sci. 63 (2012) 249. [CrossRef] [Google Scholar]
  87. C.M. Sellars et al., Mater. Sci. Eng. A 280 (2000) 1. [CrossRef] [Google Scholar]
  88. H. Hållberg et al., Comput. Mater. Sci. 49 (2010) 25. [CrossRef] [Google Scholar]
  89. C.W. Zheng et al., Comput. Mater. Sci. 44 (2008) 507. [CrossRef] [Google Scholar]
  90. F. Chen et al., Model. Simul. Mater. Sci. Eng. 17 (2009) 75015. [CrossRef] [Google Scholar]
  91. O.M. Ivasishin et al., Mater. Sci. Eng. A 433 (2006) 216. [CrossRef] [Google Scholar]
  92. R.A. Petkovic et al., Can. Met. Quart. 14 (1975) 137. [CrossRef] [Google Scholar]
  93. F. Chen et al., Model. Simul. Mater. Sci. Eng. 20 (2012) 045008. [CrossRef] [Google Scholar]
  94. R.L. Goetz et al., Scripta Mate. 38 (1998) 405. [CrossRef] [Google Scholar]
  95. N. Yazdipour et al., Comput. Mater. Sci. 44 (2008) 566. [CrossRef] [Google Scholar]
  96. H.L. Ding et al., Model. Simul. Mater. Sci. Eng. 17 (2009) 025009. [CrossRef] [Google Scholar]
  97. F. Chen, PhD thesis, Shanghai Jiaotong University, 2012. [Google Scholar]
  98. F. Chen et al., Comput. Mater. Sci. 83 (2014) 331. [CrossRef] [Google Scholar]
  99. Z. Liu et al., J. Mater. Eng. Perform. 5 (1996) 521. [CrossRef] [Google Scholar]
  100. C.W. Zheng et al., Scripta Mater. 58 (2008) 838. [CrossRef] [Google Scholar]
  101. C.W. Zheng et al., Acta Mater. 57 (2009) 2956. [CrossRef] [Google Scholar]
  102. C.W. Zheng et al., Acta Mater. 60 (2012) 4768. [CrossRef] [Google Scholar]
  103. C.W. Zheng et al., Acta Mater. 61 (2013) 5504. [CrossRef] [Google Scholar]
  104. Ø. Grong et al., Prog. Mater. Sci. 47 (2002) 163. [CrossRef] [Google Scholar]
  105. D.E. Rumelhart et al., Nature 323 (1986) 533. [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  106. M.W. Craven et al., Future Gener. Comput. Syst. 13 (1997) 211. [CrossRef] [Google Scholar]
  107. Y.C. Lin et al., Mater. Des. 32 (2011) 1733. [CrossRef] [Google Scholar]
  108. J. Kusiak et al., J. Mater. Process. Technol. 127 (2002) 115. [CrossRef] [Google Scholar]
  109. Y.C. Lin et al., Comput. Mater. Sci. 43 (2008) 752. [CrossRef] [Google Scholar]
  110. M.Q. Li et al., J. Mater. Process. Technol. 123 (2002) 377. [CrossRef] [Google Scholar]
  111. M.Q. Li et al., Mater. Charact. 49 (2003) 203. [Google Scholar]
  112. M.Q. Li et al., Mater. Sci. Eng. A 528 (2011) 2265. [CrossRef] [Google Scholar]
  113. J.H. Kim et al., Met. Mater. Int. 15 (2009) 427. [Google Scholar]
  114. Z.C. Sun et al., Comput. Mater. Sci. 50 (2010) 308. [CrossRef] [Google Scholar]

Cite this article as: Chen F, Cui Z & Chen J: Prediction of microstructural evolution during hot forging. Manufacturing Rev. 2014, 1, 6.

All Tables

Table 1.

Sellars model for different microscopic phenomena in hot working of C-Mn steel.

In the text
Table 2.

Yada model for different microscopic phenomena in hot working of C-Mn steel.

In the text
Table 3.

Phenomenological model for different microscopic phenomena in hot working of 38MnVS6(Ti) steel.

In the text
Table 4.

Phenomenological model for different microscopic phenomena in hot working of 6082 aluminum alloy.

In the text

All Figures

thumbnail Figure 1.

Schematic diagram showing the use of the phenomenology model in hot forging processes.
In the text
thumbnail Figure 2.

The flow chart of the technical routing of Sellars methodology.
In the text
thumbnail Figure 3.

Simulation results: (a) distribution of dynamic recrystallization fraction in the workpiece after finish-forging, (b) distribution of grain size of austenite in the workpiece after finish-forging, (c) distribution of ferrite in the workpiece at different time after cooling process, (d) distribution of pearlite in the workpiece at different time after cooling [27].
In the text
thumbnail Figure 4.

Comparison of the predicted values and the experimental values of the grain size at the areas A and B.
In the text
thumbnail Figure 5.

Distribution of dynamic recrystallization volume fraction (a) and grain size, (b) after finishing-forging of magnesium alloy AZ31B spur bevel gear [28].
In the text
thumbnail Figure 6.

Metalographs of the areas A, B and C in the magnesium alloy bevel gear [28].
In the text
thumbnail Figure 7.

Distribution of static recrystallized volume fraction (a) and average grain size, (b) during holding period after final-forging [29].
In the text
thumbnail Figure 8.

Metallography of the posterosuperior control arm of Zones A and B [29].
In the text
thumbnail Figure 9.

Types of periodical cellular automaton grids in two and three dimensions.
In the text
thumbnail Figure 10.

Classic neighborhood definitions.
In the text
thumbnail Figure 11.

CA simulation of the normal grain growth (a) two-dimensional CA simulation, (b) three-dimensional CA simulation.
In the text
thumbnail Figure 12.

Illustration of different sided grains (a) a four-sided grain, (b) a five-sided grain, (c) a six-sided grain.
In the text
thumbnail Figure 13.

Predicted microstructural evolution of 30Cr2Ni4MoV rotor steel at the temperature of 970 °C and strain rate of 0.1 s−1 with the CA model. The strains are: (a) 0.25, (b) 0.35, (c) 0.45 and (d) 0.5, respectively [83].
In the text
thumbnail Figure 14.

The CA model coupling the topology technology [79, 83, 84].
In the text
thumbnail Figure 15.

Comparison of the simulated, average grain-sizes after each pass, with the experimental results [79, 83].
In the text
thumbnail Figure 16.

Comparison of two simulations: (a) distribution of macroscopic quantities from the FEM simulation, and (b) mesoscale simulation results after four-pass stretching by CA simulation [83].
In the text
thumbnail Figure 17.

Schematic structure of a back propagation neural network.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.