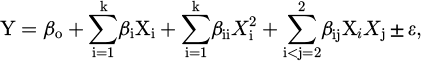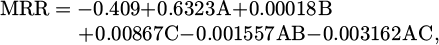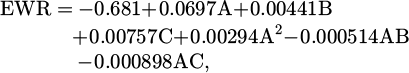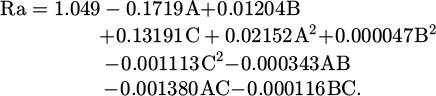| Issue |
Manufacturing Rev.
Volume 11, 2024
|
|
|---|---|---|
| Article Number | 4 | |
| Number of page(s) | 16 | |
| DOI | https://doi.org/10.1051/mfreview/2024002 | |
| Published online | 01 March 2024 | |
Research article
Modeling and analysis of process parameters in EDM of Ni35Ti35Zr15Cu10Sn5 high-temperature high entropy shape memory alloy by RSM Approach
1
Department of Mechanical Techniques, Technical Institute of Babylon, Al-Furat Al-Awsat Technical University (ATU), Najaf 54003, Iraq
2
Department of Metallurgical Engineering, College of Materials Engineering, University of Babylon, Babylon 51002, Iraq
* e-mail: mohammedali_jabur@yahoo.co; mohammed.dakhil@atu.edu.iq
** e-mail: mat.saad.hameed@uobabylon.edu.iq
Received:
17
August
2023
Accepted:
4
January
2024
The Electrical Discharge Machining (EDM) technique demonstrates proficiency in fabricating precise and intricate geometries, especially in challenging-to-machine materials like high-entropy shape memory alloys. Analyzing and optimizing machining parameters are crucial for their direct impact on mechanical properties and overall product efficiency. The main responses chosen to evaluate the processes are material removal rate (MRR), electrode wear rate (EWR), and surface roughness (Ra). At the same time, the associated machining conditions were discharge current (Ip), pulse-on time (Ton), and pulse-off time (Toff). EDM is a multi-response process; therefore, the method of Response Surface Methodology (RSM) is utilized to assess the influence of machining parameters on Ni35Ti35Zr15Cu10Sn5 (at%) high-temperature high entropy shape memory alloy (HT-HE-SMA) using a copper electrode. Based on a center composite design (CCD), experiments were analyzed using Minitab19 software. To identify the most influential parameters, a thorough analysis of variance (ANOVA) at various significance levels (5%) was performed, checking the sufficiency of all fitted second-order regression models. Discharge current, pulse-on time, and pulse-off time were identified as significant factors that affect output (MRR, EWR, and Ra). The model adequacy of the current experimental investigation is perfect, with determination coefficients (R2) of 97.82% for MRR, 95.36% for EWR, and 99.53% for Ra.
Key words: Ni-Ti-Zr-Cu-Sn (HT-HE-SMA) / EDM / CCD / RSM / ANOVA
© M.A. Al-Mousawi et al., Published by EDP Sciences 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Every day, traditional materials are gradually being replaced by newer, more advanced engineering materials in parallel with the development of technology. From the moment shape memory alloys (SMAs) were discovered, they have garnered substantial interest from researchers and commercial sectors alike. Their unique characteristics of shape memory effect (SME) and superelasticity (SE) make them highly sought-after materials for diverse applications [1–3]. Also, since the initial breakthroughs achieved by Yeh, Cantor, and their associates in 2004, high entropy alloys, often known as HEAs, have been at the front of cutting-edge technological materials. They've been the subject of much research lately due to their unique and appealing characteristics [4]. High Entropy Alloys (HEAs) are alloys with a minimum of five primary elements and a constituent element concentration ranging from 5 to 35 at% [5]. Despite having many alloying elements, HEAs can form a single solid solution phase [6].
Combining the properties of shape memory alloys and high entropy alloys presents an exciting opportunity for creating materials with novel properties but poses significant challenges [7–9].
In comparison to traditional shape-memory alloys (SMAs), High-Entropy Shape Memory Alloys (HESMAs) have the ability to provide much better characteristics and property combinations than conventional alloys, for instance, exhibit enhanced yield strength and a broader phase transition temperature range [10–14]. These improvements can be attributed to significant lattice distortion and sluggish diffusion [15,16]. These remarkable characteristics facilitate the utilization of high-entropy shape-memory alloys across a broader spectrum of applications.
HE-SMAs can be utilized as components for electronics coatings, tools, nozzles, stamping presses, refractory constructions, nuclear power plants, chemical plants, marine structures, and engines (including aircraft engines) [17–19]. The electronic, electrical, thermoelectric, electromagnetic, and medical areas could also use it [20]. This functional material presents significant machining challenges due to its varied shape memory properties that are temperature-dependent, its super elasticity, and the pronounced increase in hardness due to strong work hardening, which makes using traditional machining techniques difficult [1,21,22]. Their characteristics can often make them difficult to machine. Materials that are challenging to process are the focus of unconventional machining techniques such as electrochemical machining (ECM), ultrasonic machining (USM), electrical discharging machine (EDM), recently created hybrid machining, etc. [23].
The method of electrical discharge machining operates through the utilization of a mechanism known as spark erosion, and it possesses the capability to fabricate complex geometries with exceptional accuracy in materials that are challenging in hard-to-machine. It is a method that uses high-frequency electric sparks for electro-erosion purposes and removes material from a surface by repeatedly melting, evaporating, and solidifying it. Difficult-to-machine materials are processed without considering their physical, mechanical, or metallurgical properties [24,25]. When employing HE-SMAs in practical applications components, it must be assured that they are safe to manufacture and process. There haven't been many books or articles about the machining of HEAs components up to the present, and there is no systematic knowledge concerning the safe and reliable machining of these materials [26,27]. Therefore, this study aims to investigate the MRR, EWR, and Ra of EDMed parameters and evaluate conceivable modifications in relation to the parameters it possesses. In order to use statistical methods to achieve higher MRR, smaller EWR, and Ra. The experiments are employed in this study to consider the impacts of the Ip, Ton, and Toff on MRR, EWR, and Ra.
2 Experimental details
The studies were conducted using an electrical discharge machine (EDM). (CHMER, Die-sinking EDM, CNC) It functions using an ISO-pulse in the dielectric medium of kerosene. In this study, the workpiece material utilized was a high-temperature high entropy shape memory alloy (HT-HE-SMA) characterized by an atomic composition of 35%Ni – 35%Ti – 15%Zr – 10%Cu – 5%Sn, (at.), which was synthesized through the powder metallurgy method. The synthesis process involved 80 hours of mechanical alloying, utilizing an eccentric rotary ball mill. This involved employing jars and balls constructed from hardened alloy steel (AISI 52100) with a hardness of 63 HRC, a ball-to-powder weight ratio of 1:15, and a rotational speed of 150 rpm in alternating directions. The addition of 1.5% stearic acid served to regulate the cold-welding effect and improve the efficiency of the ball milling process. The atmospheric conditions were maintained at 1 bar of argon pressure. Subsequently, the resulting powder underwent sintering at 1100 °C for one hour within a vacuum tube furnace. The resultant samples demonstrated an average hardness of 1200 MPa. The distribution of elements in the sintered sample is illustrated in Figure 1 by Scanning electron microscopy (SEM) elemental mapping elemental mapping with energy dispersive spectroscopy (EDS). The average hardness (1200 MPa). The workpiece was a specimen having a diameter of 10 mm and thickness of 5 mm as illustrated in Figure 2 and 1.5 µm for surface roughness Ra. Cylindrical copper electrodes 60 mm long and 10.5 mm in diameter were positioned along the axis of the workpiece and utilized as positive polarity electrodes as illustrated in Figure 3. The workpiece to electrode gap was 10 μm, and the depth of cut was 0.6 mm. The characteristics and levels described in Table 1 were chosen based on the scope of EDM machines (Fig. 4).
A digital balance (Denver Instruments) was used to measure the weight of the workpiece and electrode with an accuracy of 0.01 mg or less. Following the EDM procedure, the weight loss of the workpiece and electrode was measured and utilized to estimate the MRR and EWR. Calculating the roughness profile using its mean deviations along the measurement path, starting at the center line to characterize the surface condition of each workpiece. The Maher Company's portable stylus profile meter, Pocket Surf (III/PMD 90101), was utilized to evaluate surface roughness.
The machined samples underwent for cleaning process using acetone solvent, followed by a drying step with a hot air blower before being measured for Ra. In order to ensure validity and precision, each Ra calculation was repeated six times in each of the six different orientations, and the roughness value for each treatment combination was established as the average sum of the six replications.
To investigate the characteristics of both samples, they are subjected to an electro-polishing procedure to treat the surfaces as well as the sub-surfaces, after which they are examined using a scanning electron microscope with EDX mapping (SEM model; Axia ChemiSEM, Thermo Fisher Scientific Inc.).
 |
Fig. 1 Ni35Ti35Zr15Cu10Sn5 high entropy shape memory alloy. |
 |
Fig. 2 The workpiece of HE-SMAs. |
 |
Fig. 3 Copper electrodes. |
Independent input Parameters, Coded and Actual levels.
 |
Fig. 4 CNC, CHMER EDM. |
3 Mathematical modeling based on RSM
The second-order model is usually applied when the response function is unknown or non-linear. A second-order model has been used in the current investigation; after analyzing the experimental results, a mathematical model was built to depict the correlation between the process variable and the response. The second-order model, as represented by equation (1) provides the explanation for the system's behavior.
where Y represents the response, Xi represents the input variables, and Xi2 and XiXj, the input variables, are represented by their corresponding squares and interaction terms, respectively. The regression coefficients that are not known are represented by the symbol. o, i, ij, and ii, and the model's error is shown as.
Statistical regression analysis of the experimental data acquired by Table 2 allowed the relationship between the MRR, EWR, and Ra, and the other process parameters will be investigated. Acceptance was determined by evaluating high measurements to extremely high correlation coefficients for non-linear and linear regression models. A polynomial regression model was employed to model each of the three factors under consideration in this evaluation. A quadratic model incorporating MRR, EWR, and Ra has been proposed, as indicated in equation (1) and according to the results of experiments, the regression model's coefficients can be computed using the experimental observations. These variables' effects and interactions were considered in this investigation, and the resulting model is expressed as an equation that represents the interaction. Table 3 summarizes the results after the backward elimination method.
Paper All three input parameters (A: discharge current, B: pulse-on time, and C: pulse-off time) have essential effects on Table 3, with at least a 0.05 level of significance or (95%) confidence interval, and P-values for all responses (MRR, EWR, and Ra) were close to zero. The more significant the influence was, the smaller the P-value, a term commonly used in statistical modeling language [28]. The second way pulse current and pulse-on time interact (A×B) and pulse current and pulse-off time interact (A×C) has more of an impact on MRR. For measuring EWR, the interactive effects of pulse current and pulse-on time (A×B) and the interactive effects of pulse current and pulse-off time (A×C), as well as the second-order impacts of pulse current (A2), were found to affect the results. Finally, the pure quadratic effects of pulse current (A2), pulse-on time (B2), and pulse-off time (C2), as well as the interactions between pulse current and pulse-on time (A×B), pulse current and pulse-off time (A×C), and pulse-off time (BC), and pulse-on time, were also discovered to be significant factors in determining Ra.
Table 4 presents the ANOVA outcomes for the model's three response functions with a confidence level of 95%. It was noted that all quadratic regression models display either a higher level of significance (P-value = 0) or a significant level between (0 < P-value < 0.05), except for A2, B2, C2, and B × C for MRR, B2, C2, and B × C for EWR (P-value > 0.05), as well as all models adequately capture data from experiments. The lacks of fits for Ra transpired to be insignificant in relation to the pure error. As a result, the sufficiency of the model verification for the Ra output measure is completely ensured.
Ordinary R-squared is another statistical diagnostic index that is mainly used to assess the model's goodness of fit, the representation of R-squared (R2), adjusted R-squared (R2adj.), and predicted R-squared (R2pred.) [29], The model for each response can be found in Table 4. The values under consideration are 97.82%, 97.05%, and 91.05% for MRR; 95.36%, 93.22%, and 83.4% for EWR; and 99.53%, 99.11%, and 96.21% for Ra, respectively. Generally, the more accurate the R2s are to unity, the more closely the model matches experimental data [30,31]. Standard statistic R2, also called the multiple determination coefficient, expresses the proportion of the model's total variations that can explained. While the R2adj. Statistic, which is adjusted for the model's size (number of components), indicates the percentage of total variability that the model can explain after accounting for significant terms (in the reduced model); the value of R2 increases with every additional variable or regressor incorporated into the model, whether significant or insignificant.
On the contrary, the adjusted R2 does not necessarily increase when additional predictor variables are introduced into the model. In reality, the value of R2adj. will frequently diminish when superfluous terms are included. So, when R2 and R2adj. are very different, there is a good chance that the model incorporates terms that are not significant [30,31]. Hence, it's an appropriate standard for assessing a model's goodness of fit when it includes only significant terms compared to the scenario where all terms are caught up.
Table 5 lists the finalized values for each regression coefficient for each response. The experimental outcomes enhancements to regression (prediction) equations to each response attribute (MRR, EWR, and Ra) in relation to the three EDM parameters as a function, as shown below. Some terms of the quadratic equations (2)–(4) have had their unimportant coefficients deleted.
Planned methodology and actual experimental.
Model Parameters and Regression Coefficients for MRR, EWR, and Ra.
ANOVA and fit summary for the second-order models of MRR, EWR, and Ra.
Response model finalized regression coefficients.
4 Results and discussion
4.1 Parametric analysis of EDM parameters on MRR
The main influence plot of the MMR for every variable, as illustrated in Figure 5. The MRR can be seen to increase gradually as the discharge current rises. The erosion rate is increased because higher discharge currents cause greater amounts of electrical discharges that can remove a larger amount of material from the workpiece [32]. There's a decrease in the MRR as the pulse-on time increases. Despite common opinion, shorter pulse-on times actually allow for more electrical discharge to occur than longer ones; when the pulse duration is increased, the plasma channel enlarges excessively, which diminishes the efficiency of plasma flushing and the density of electrical discharge happening within the gap space. This is coupled with an increased resolidification of the molten material instead of it being effectively removed [33,34]. On the other hand, the most important influence of pulse-off time demonstrates a tendency to behave in the opposite direction. As the pulse-off time increases, the plasma channel shrinks, reducing the attack of positive ions on the workpiece surface and lowering the MRR. Significantly, these results were determined by examining the impact of each factor independently (while maintaining the constant of the other parameters); however, more practically useful insights can be unveiled when the collective effects of these factors are studied simultaneously; this can be accomplished by examining 3D surface and 2D contour plots of response metrics in connection with each significant pair of input variables.
Figures 6a and 6b illustrate the combined effect of discharge current (A) and pulse-on time (B) at a steady middle value of pulse-off time (C) in both 3D surface and 2D contour presentations. The upper left area of the contour plot demonstrates that maximum material removal rates (MRRs) can be achieved when the discharge current reaches its peak and the pulse-on time is set to its lowest permissible values within the scope of process parameters investigated in this study. The influence that current (A) and pulse-off-time (C) have on MRR is seen in Figures 6c and 6d. It is common knowledge that while keeping the pulse-on time at certain levels, which in this situation is the level at medium, higher MRR amounts can be attained mainly in the region identified by a high current and a low pulse off-time. A rise in Ip generates a powerful spark, and when Toff decreases, the workpiece's temperature doesn't significantly drop before the ignition of the next spark, leading to an increased material removal rate (MRR). An exhaustive analysis of residuals has been performed for each formulated response, with the corresponding graphs illustrated in Figure 7.
The normal probability plot is a visual method used to assess if a dataset closely follows a normal distribution. The normal probability plot of residuals indicates that the experimental data roughly aligned along a straight line, validating a strong correlation between the observed and predicted values for the response (Fig. 7a). Only minor fluctuations are noticeable in the plot of residuals versus fitted values (Fig. 7b). The histogram of residuals in Figure 7c displays a Gaussian distribution, indicating that the error frequency falls within the −0.5 to 0.3 range, which is desirable. Finally, the plot of residuals against the order of experiments can be seen in Figure 7d. Both negative and positive residuals suggest no specific trend, which is statistically significant.
 |
Fig. 5 Main effect plots for MRR. |
 |
Fig. 6 3D response surface plot and contour plot of EDM parameters on MRR. |
 |
Fig. 7 Residual plots for MMR. |
4.2 Parametric analysis of EDM parameters on EWR
Figure 8 illustrates the graphical representation of the three primary effects plot of the EWR model, each of which was created with the other parameters held constant at the median level. A similar pattern is observed when comparing the main effect plots of MRR. The EWR increases with increased discharge current and can reach up to 0.4673 g/min on its own. This is the highest amount of EWR in these graphs, confirming that the discharge current, above all other parameters, has the most significant influence on EWR. It's evident from the main effect plot of pulse-on time that establishing longer pulse-on times can be beneficial, as shorter pulse durations can contribute to tool wear, while shorter pulse durations will decrease tool wear. Figure 9 illustrates a single electrical discharge with constant polarity across the two electrodes and the created plasma channel. Accelerating electrons bombard the anode surface (positive pole: tool) with each discharge, while ions attempt to migrate towards the cathode, which is the negatively charged (negative pole: workpiece); they collide with the work material's surface. With short pulse durations, it has the opportunity to activate large amounts of negatively charged particles, which are thousands of times lighter than ions, to strike the tool's positive (anode) electrode, which helps to increase the erosion rate of the electrode material [35]. Finally, choosing a higher Toff results in a smaller EWR. This is the same justification for the MRR, which can be applied here while maintaining other variables unchanged.
Figures 10 a and 10b depicts the EWR response surface plot and its related contour plot for current (A) and pulse-on time (B). Lower electrode wear rates (EWRs) are always desirable, and they can be achieved by utilizing reduced discharge currents in combination with extended pulse-on times (as seen on the upper left side of the contour diagram). Lengthening the pulse duration allows heavier positive ions to reach the target workpiece on the cathode, controlling the plasma channel trajectory and safeguarding the anode tool from damage caused by excited electrons [36]. Additionally, due to the elevated plasma temperature during sparking, the carbon emitted from the breakdown of hydrocarbon-based dielectric fluid adheres to the tool's surface, forming a wear-resistant coating.
This subsequently results in a notable reduction in EWR during periods of extended pulse duration [37].
Figures 10 c and 10d show how Ip and Toff affect the predicted response surface and contour plot of EWR, with Ton remaining constant in their middle level. It is important to note that the EWR gets lower as the Ip gets lower with increasing Toff, and EWR decreases as a lower Ip fails to generate a potent spark, coupled with the cooling effect induced by a high Toff.
The residual plots of EWR (Fig. 11a) indicate a normal distribution of residuals with minimal deviation, underscoring the appropriateness of the predictive model. Moreover, the residuals don't follow any consistent pattern and are randomly dispersed around zero, regardless of the magnitude of the fitted values. The residual vs. fitted value plot (Fig. 11b) shows that the residuals are relatively small and decrease as the fitted values increase. The histogram of residuals in Figure 11c displays a Gaussian distribution, indicating that the error frequency falls within the −0.1 to 0.075 range, which is optimal, and the Residual vs. observation order plot (Fig. 11d) shows no observable time trend or inclination towards lower values in the model. This proves that the model did not underestimate MRR values.
 |
Fig. 8 Main effect plots for EWR. |
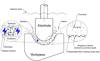 |
Fig. 9 Electrical discharge diagram. |
 |
Fig. 10 3D response surface plot and contour plot of EDM parameters on EWR. |
 |
Fig. 11 Residual plots for EWR. |
4.3 Parametric analysis of EDM parameters on Ra
The effects of varying input parameters, such as those seen in Figure 12, are pulse current, pulse-on time, and pulse-off time on surface roughness. Surface roughness increases as discharge current increases. The rise in surface roughness is caused by an increase in spark energy, which causes the surface pits that result from material removal to expand. Similarly, Ra augmented in tandem with an escalation in Ton, transitioning from a minimum to a maximum level, with all other parameters remaining constant at their intermediate values. When the expulsion pressure is held steady, the insulating fluid is incapable of clearing away the molten substance from the sample, which results from long Ton. Furthermore, there is a minor increase of 0.231 µm in Ra, Toff elevates from 25 to 50 µs, while it sees a reduction of 0.605 when Toff is increased from 50 to 75 µs.
The combined effects of pulse current (A) and pulse-on time (B) on Ra are shown in Figure 13a. It becomes evident that reducing the pulse-on time leads to smaller values for Ra discharge current, which can produce smoother surfaces, known as a low energy state. However, reducing their variation ranges to minimum values may achieve more smooth surfaces. The contour diagram and the response surface to Ra are in with the machining parameters Ip and Ton, where Ra tends to increase substantially as Ip increases for any given Ton value, as shown in Figure 13b. Hence, the lowest Ra is attained with a reduced peak current (8 A) and pulse-on time (50 μs). Due to their ability to control input energy, a surge in Ip will melt more material and be worn away from the workpiece due to a more powerful spark, leading to larger craters and higher temperatures.
Figures 14a and 14b illustrates the prediction of Ra's response surface and contour under the impact of Ip and Toff, while Ton is maintained at a steady 100 μs level. Notably, as Ip rises, it also increases Ra; the rationale for this is, as previously mentioned. However, Ra decreases gradually with an increase in Toff, particularly at lower Ip levels, while at higher Ip, Ra escalates. It's worth noting that Toff's influence is considerably less than Ip and Ton's. In conclusion, Figures 14c and 14d displays Ra as a function of Ton and Toff, with Ip fixed at 12 A. Based on these findings, it can be deduced that both Ip and Ton share a proportional relationship with Ra, and in comparison, to these parameters, Toff's impact is minimal within the experimental range that was utilized for this test.
As demonstrated in Figure 15a, the normal distribution of residuals affirms the appropriateness of the predictive model used. Moreover, in Figure 15b, it can be observed that the residuals lack any discernible pattern and are randomly dispersed, regardless of the magnitude of the fitted values. The histogram of residuals depicted in Figure 15c demonstrates a Gaussian distribution, indicating that the errors are well-distributed within the range of −0.125 to 0.075, which is considered desirable. The Residual vs. observation order plot (Fig. 15d) shows no discernible trend or drift in the model. This proves that the model has not underestimated the Ra values. As a whole, none of the yielded models show any inadequacy.
 |
Fig. 12 Main effect plots for Ra. |
 |
Fig. 13 3D response surface plot and contour plot of EDM parameters on Ra. |
 |
Fig. 14 3D response surface plot and contour plot of EDM parameters on Ra. |
 |
Fig. 15 Residual plots for Ra. |
4.4 The results of scanning electron microscopy (SEM)
The EDM process is highly intricate and fast-paced, involving rapid localized heating and cooling, along with the random action of the spark. Consequently, a thermally affected layer is formed on the workpiece surface due to melting and resolidification, which is not expelled or removed by flushing. This layer, known as the white layer, possesses a distinct structure from the original material and is characterized by a fine-grained and hard nature. One can find globules, cracks, and microcracks within the white layer, and their density is contingent on the process conditions. The structure of this surface contributes to an increase in roughness, which Ip heavily influences. The impact of EDM parameters on the formation of craters and rough surfaces during the EDM process can be distinctly seen in the SEM micrographs under varied parameter combinations.
The scanning electron microscope examination showed that the surface has a complicated appearance and that it is enclosed with spherical particles, shallow craters, molten droplets, pockmarks, debris globules, and voids, which are the result of the high thermal energy released by discharges followed by rapid cooling. The spherical particles are molten metals that are randomly discharged during the process, which then solidify and adhere to the surface. Figure 16 shows SEM photograph of Ni35Ti35Zr15Cu10Sn5 (HT-HE-SMAs). This occurs at different levels of Ip, Ton, and Toff, as referenced in the accompanying figure descriptions.
The sample labeled with the symbol (A) exhibits the greatest amount of metal removal rate, accompanied by a roughness level that approaches the highest observed roughness in the processes; whereas the sample containing the symbol (b) exhibits a moderate metal removal rate, as well as a slightly elevated roughness; while the sample exhibiting the lowest metal removal rate in the processes, characterized by a roughness level that is approximately moderate, is denoted by the symbol (C); another instance may be observed in the symbol (D) is utilized, indicating that the surface roughness is at its minimum level during the experiments. Additionally, the metal removal rate associated with this process is lower compared to the average.
The variation forms of crater rims, microcracks, and globular attachments can be seen in the figures corresponding to diverse machining parameters. A significant enlargement of the crater and microcracks in the samples is evident because an increase in spark energy with pulse currents leads to a higher surface crack density and deeper, broader craters on the surface. However, the crater's diameter is also affected by Ton and expands with its increase. Subsequently, as Ton increases to some extent, more heat is provided over a longer duration, producing more molten material with larger globules and craters. During the cooling process, thermal stress is created, leading to an increase in the density of surface cracks. Consequently, the length of the surface cracks experiences an increase. When the duty cycle is increased, the outcome is a greater density of surface cracks due to inadequate heat dissipation to the surrounding environment. This leads to oxidation and an increase in the thickness of the recast layer. Whereupon, the recast layer exhibits reduced thermal and electrical conductivity, resulting in a decrease in the rate of metal removal and an increase in surface roughness. Additionally, the effect of Toff initially experiences a slight increase before subsequently decreasing [38–40].
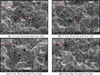 |
Fig. 16 SEM photograph of Ni35Ti35Zr15Cu10Sn5 (HT-HE-SMAs) at various levels of Ip, Ton and Toff. |
5 Conclusion
In this study on the EDM of high-temperature high entropy shape memory alloy (HT-HE-SMA), a second-order RSM model was developed to analyze the significant effects of Ip, Ton, and Toff, including their quadratic implications and interactions, on MRR, EWR, and Ra. The research findings underscore that the machining input parameters have a critically significant influence. Based on the experimental results and response model, the ensuing conclusions can be deduced:
In terms of the analysis of main effects, the MRR and EWR behave similarly, though the MRR and EWR behave more nonlinearly. Increasing either Ip results in greater MRR and EWR values, whereas increasing Ton or Toff causes the reverse effect. On the other hand, the work roughness value, Ra, is directly proportional to both the Ip and Ton while Ra increases slightly from low to middle and then decreases to high level when Toff increases.
The two-way interaction effects of Ip with Ton (A×B) and Toff (A×C) have significantly controlled the MRR.
On the EWR measure, the same dual interaction effects that influenced the MRR and plus the pure quadratic effects of Ip (A2) were found to be statistically significant.
The pure quadratic and the parameters' interaction effects are significant for the Ra response.
The enlargement of the crater dimensions and the presence of micro-cracks in the specimens are attributed to the escalation in spark energy resulting from the application of pulse currents.
Utilizing RSM models, this research provides insights for enhancing the EDM efficiency of Ni35Ti35Zr15Cu10Sn5 HT-HE-SMA, offering a robust approach for precise machining and a predictive equation for MRR, EWR, and Ra, corroborated by R2 values of 97.82% for MRR, 95.36% for EWR, and 99.53% for Ra, match between experimental and predicted values.
Funding
This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
Conflict of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Data availability
All data generated and analyzed during this study are included in this article.
Author contribution statement
Conceptualization, Al-Mousawi, Al-Shafaie and Khulief; data collection, Al-Mousawi; Methodology, Al-Mousawi and Al-Shafaie; Software, Al-Shafaie and Al-Mousawi; Validation, Al-Mousawi, Al-Shafaie and Khulief; Formal Analysis, Al-Shafaie and Al-Mousawi; Investigation, Al-Mousawi; Resources, Al-Mousawi; Data Curation, Al-Mousawi and Al-Shafaie; Writing – Original Draft Preparation, Al-Shafaie and Al-Mousawi; Writing – Review & Editing, Al-Mousawi. All authors reviewed the results and approved the final version of the manuscript.
References
- J. Mohd Jani, M. Leary, A. Subic, M.A. Gibson, A review of shape memory alloy research, applications and opportunities, Mater. Des. 56 (2014) 1078–113 [CrossRef] [Google Scholar]
- C. Dimitris, Lagoudas. Shape memory alloys: modeling and engineering applications. 2008 th edn. Springer, 2008 [Google Scholar]
- K. Otsuka, C.M. Wayman, Shape memory materials, Cambridge University Press, 1999 [Google Scholar]
- A. Günen, F. Ceritbinmez, K. Patel, M.A. Akhtar, S. Mukherjee, E. Kanca et al., WEDM machining of MoNbTaTiZr refractory high entropy alloy, CIRP J. Manuf. Sci. Technol. 38 (2022) 547–559 [CrossRef] [Google Scholar]
- R. Sabban, K. Dash, S. Suwas, B.S. Murty, Strength-ductility synergy in high entropy alloys by tuning the thermo-mechanical process parameters: a comprehensive review, J. Indian Inst. Sci. 102 (2022) 91–116 [CrossRef] [Google Scholar]
- T. Richter, D. Schröpfer, M. Rhode, A. Börner, Influence of modern machining processes on the surface integrity of high-entropy alloys, IOP Conf. Ser. Mater. Sci. Eng. 882 (2020) 012016 [CrossRef] [Google Scholar]
- G.S. Firstov, T.A. Kosorukova, Yu.N. Koval, V.V. Odnosum, High entropy shape memory alloys, Mater. Today Proc. 2 (2015) S499–S503 [CrossRef] [Google Scholar]
- G.S. Firstov, T.A. Kosorukova, Y.N. Koval, P.A. Verhovlyuk, Directions for high-temperature shape memory alloys' improvement: straight way to high-entropy materials? Shape Mem. Superelasticity 1 (2015) 400–407 [CrossRef] [Google Scholar]
- D. Piorunek, J. Frenzel, N. Jöns, C. Somsen, G. Eggeler, Chemical complexity, microstructure and martensitic transformation in high entropy shape memory alloys, Intermetallics (Barking) 122 (2020)106792 [CrossRef] [Google Scholar]
- S. Li, D. Cong, X. Sun, Y. Zhang, Z. Chen, Z. Nie et al., Wide-temperature-range perfect superelasticity and giant elastocaloric effect in a high entropy alloy, Mater. Res. Lett. 7 (2019) 482–489 [CrossRef] [Google Scholar]
- G. Zhao, D. Li, G. Xu, D. Fang, Y. Ye, C. Huang et al., As-cast high entropy shape memory alloys of (TiHfX)50(NiCu)50 with large recoverable strain and good mechanical properties, J. Mater. Eng. Perform. 31 (2022) 10089–10098 [CrossRef] [Google Scholar]
- S.-Y. Kuo, W.-P. Kao, S.-H. Chang, T.-E. Shen, J.-W. Yeh, C.-W. Tsai, Effect of homogenization on the transformation temperatures and mechanical properties of Cu15Ni35Hf12. 5Ti25Zr12.5 and Cu15Ni35Hf15Ti20Zr15 high-entropy shape memory alloys, Materials 16 (2023) 3212 [CrossRef] [Google Scholar]
- E.J. Pickering, N.G. Jones, High-entropy alloys: a critical assessment of their founding principles and future prospects, Int. Mater. Rev. 61 (2016) 183–202 [CrossRef] [Google Scholar]
- Y. Zhang, T.T. Zuo, Z. Tang, M.C. Gao, K.A. Dahmen, P.K. Liaw et al., Microstructures and properties of high-entropy alloys, Prog. Mater. Sci. 61 (2014) 1–93 [CrossRef] [Google Scholar]
- P. Sharma, V.K. Dwivedi, S.P. Dwivedi, Development of high entropy alloys: a review, Mater. Today Proc. 43 (2021) 502–509 [CrossRef] [Google Scholar]
- E.P. George, D. Raabe, R.O. Ritchie, High-entropy alloys, Nat. Rev. Mater. 4 (2019) 515–534 [CrossRef] [Google Scholar]
- J.-W. Yeh, Alloy design strategies and future trends in high-entropy alloys, JOM 65 (2013) 1759–1771 [CrossRef] [Google Scholar]
- B.S. Murty, J.-W. Yeh, S. Ranganathan, P.P. Bhattacharjee, High-entropy alloys, 2nd edn. Elsevier, Amsterdam, 2019 [Google Scholar]
- D.O. Svensson, High entropy alloys: breakthrough materials for aero engine applications? Diploma work in the Master programme, Appl. Phys., nd, [Google Scholar]
- M.-H. Tsai, J.-W. Yeh, High-entropy alloys: a critical review, Mater. Res. Lett. 2 (2014) 107–123 [CrossRef] [Google Scholar]
- K. Weinert, V. Petzoldt, Machining of NiTi based shape memory alloys, Mater. Sci. Eng. A 378 (2004) 180–184 [CrossRef] [Google Scholar]
- F. Ceritbinmez, A. Günen, M.A. Akhtar, K. Patel, S. Mukherjee, L. Yünlü et al., Surface integrity characteristics in wire-EDM of HfTaTiVZr refractory high entropy alloy, Adv. Mater. Process. Technol. (2022) 1–18. [Google Scholar]
- J. Kumar, S. Sharma, J. Singh, S. Singh, G. Singh, Optimization of wire-EDM process parameters for Al-Mg-0. 6Si-0.35Fe/15%RHA/5%Cu hybrid metal matrix composite using TOPSIS: processing and characterizations, J. Manuf. Mater. Process. 6 (2022) 150 [Google Scholar]
- M. Umar Farooq, M. Pervez Mughal, N. Ahmed, N. Ahmad Mufti, A.M. Al-Ahmari, Y. He, On the Investigation of surface integrity of Ti6Al4V ELI using si-mixed electric discharge machining, Materials 13 (2020) 1549 [CrossRef] [Google Scholar]
- M.U. Farooq, S. Anwar, M.S. Kumar, A. AlFaify, M.A. Ali, R. Kumar et al., A novel flushing mechanism to minimize roughness and dimensional errors during wire electric discharge machining of complex profiles on Inconel 718, Materials 15 (2022) 7330 [CrossRef] [Google Scholar]
- J. Guo, M. Goh, Z. Zhu, X. Lee, M.L.S. Nai, J. Wei, On the machining of selective laser melting CoCrFeMnNi high-entropy alloy, Mater. Des. 153 (2018) 211–20 [CrossRef] [Google Scholar]
- A. Polishetty, M.M.R. Barla, G. Littlefair, D. Fabijanic, Machinability assessment of multi component high entropy alloys.METMG 2015: Proceedings of the Manufacturing Engineering and Technology for Manufacturing Growth 2015 International Conference 2015, 2015 [Google Scholar]
- M. Kunieda, B. Lauwers, K.P. Rajurkar, B.M. Schumacher, Advancing EDM through fundamental insight into the process, CIRP Ann. 54 (2005) 64–87 [CrossRef] [Google Scholar]
- H.F. Mahdy, M.A. Al-Kinani, S.H. Al-Shafaie, R.M. Jailawi, Mathematical modeling for performance measure on the electrical discharge machining of inconel 718 by response surface methodology, J. Mech. Eng. Res. Dev. (2021) 44 [Google Scholar]
- C. Douglas, Montgomery. Design and analysis of experiments, 10th ed. Wiley, 2019 [Google Scholar]
- S.H.A.-S. Saad Hameed Al-Shafaie, Optimization of tool wear for turning operation based the response surface methodology, Int. J. Mech. Prod. Eng. Res. Dev. 8 (2018) 391–396 [Google Scholar]
- E.C. Jameson, Electrical discharge machining, Society of Manufacturing Engineers, 2001 [Google Scholar]
- S.H. Al-Shafaie, Prediction of MAF parameters for AISI 316 SS using RBFNN and ANN based Box-Behnken design, J. Eng. Appl. Sci. 17 (2017) 7951–7958 [Google Scholar]
- S. Assarzadeh, M. Ghoreishi, Neural-network-based modeling and optimization of the electro-discharge machining process, Int. J. Adv. Manuf. Technol. 39 (2008) 488–500 [CrossRef] [Google Scholar]
- E. Iuras, Experimental contributions regarding numerical modeling of the relative wear of the tool-electrode at EDM process, Int. J. Mater. Forming 1 (2008) 1351–1354 [CrossRef] [Google Scholar]
- A. Ozgedik, C. Cogun, An experimental investigation of tool wear in electric discharge machining, Int. J. Adv. Manuf. Technol. 27 (2006) 488–500 [CrossRef] [Google Scholar]
- H.T. Sánchez, M. Estrems, F. Faura, Development of an inversion model for establishing EDM input parameters to satisfy material removal rate, electrode wear ratio and surface roughness, Int. J. Adv. Manuf. Technol. 57 (2011) 189–201 [CrossRef] [Google Scholar]
- V. Prakash, P. Kumar, P. Singh, M. Hussain, A. Das, S. Chattopadhyaya, Micro-electrical discharge machining of difficult-to-machine materials: a review, Proc. Inst. Mech. Eng. B J. Eng. Manuf. 233 (2019) 339–370 [CrossRef] [Google Scholar]
- H.T. Lee, T.Y. Tai, Relationship between EDM parameters and surface crack formation, J. Mater. Process. Technol. 142 (2003) 676–683 [CrossRef] [Google Scholar]
- S.L. Chen, S.F. Hsieh, H.C. Lin, M.H. Lin, J.S. Huang, Electrical discharge machining of a NiAlFe ternary shape memory alloy, J. Alloys Compd. 464 (2008) 446–451 [CrossRef] [Google Scholar]
Cite this article as: Mohammed Ali Al-Mousawi, Saad Hameed Al-Shafaie, Zuheir Talib Khulief, Modeling and analysis of process parameters in EDM of Ni35Ti35Zr15Cu10Sn5 high-temperature high entropy shape memory alloy by RSM Approach, Manufacturing Rev. 11, 4 (2024)
All Tables
All Figures
 |
Fig. 1 Ni35Ti35Zr15Cu10Sn5 high entropy shape memory alloy. |
| In the text | |
 |
Fig. 2 The workpiece of HE-SMAs. |
| In the text | |
 |
Fig. 3 Copper electrodes. |
| In the text | |
 |
Fig. 4 CNC, CHMER EDM. |
| In the text | |
 |
Fig. 5 Main effect plots for MRR. |
| In the text | |
 |
Fig. 6 3D response surface plot and contour plot of EDM parameters on MRR. |
| In the text | |
 |
Fig. 7 Residual plots for MMR. |
| In the text | |
 |
Fig. 8 Main effect plots for EWR. |
| In the text | |
 |
Fig. 9 Electrical discharge diagram. |
| In the text | |
 |
Fig. 10 3D response surface plot and contour plot of EDM parameters on EWR. |
| In the text | |
 |
Fig. 11 Residual plots for EWR. |
| In the text | |
 |
Fig. 12 Main effect plots for Ra. |
| In the text | |
 |
Fig. 13 3D response surface plot and contour plot of EDM parameters on Ra. |
| In the text | |
 |
Fig. 14 3D response surface plot and contour plot of EDM parameters on Ra. |
| In the text | |
 |
Fig. 15 Residual plots for Ra. |
| In the text | |
 |
Fig. 16 SEM photograph of Ni35Ti35Zr15Cu10Sn5 (HT-HE-SMAs) at various levels of Ip, Ton and Toff. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.